题目内容
12．
如图，将△ABC的顶点A沿DE直线折叠，如图，当点A落在原△ABC外部时，探求∠1，∠2与∠A的数量关系．
分析 先根据图形翻折变换的性质得出∠A=∠A′，再根据三角形外角的性质进行解答即可．
解答 解：∠1=2∠A′+∠2，
∵△A′ED是△AED翻折变换而成，
∴∠A=∠A′，
∵∠AFE是△A′DF的外角，
∴∠AFE=∠A′+∠2，
∵∠1是△AEF的外角，
∴∠1=∠A+∠AFE，即∠1=∠A+∠A′+∠2=2∠A′+∠2．
点评 本题考查的是图形翻折变换的性质及三角形外角的性质，根据图形翻折变换的性质得出∠A=∠A′是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
2．
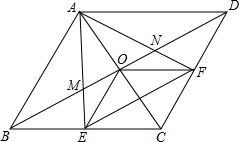如图，在菱形ABCD中，对角线AC与BD相交于点O，∠ABC=60°，点E，F分别是BC，CD的中点，BD分别与AE，AF相交于点M，N，连接OE，OF，下列结论：（1）△AEF是等边三角形；（2）四边形CEOF是菱形；（3）OF⊥AE；（4）BM=MN=ND．其中正确的结论有（ ）
如图，在菱形ABCD中，对角线AC与BD相交于点O，∠ABC=60°，点E，F分别是BC，CD的中点，BD分别与AE，AF相交于点M，N，连接OE，OF，下列结论：（1）△AEF是等边三角形；（2）四边形CEOF是菱形；（3）OF⊥AE；（4）BM=MN=ND．其中正确的结论有（ ）| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
7．物体在前一半路程的速度是6m/s，后一半路程的速度为4m/s，物体运动的平均速度为（ ）
| A． | 5m/s | B． | 4.8m/s | C． | 17.5m/s | D． | 16.7m/s |
17．有两个一元二次方程M：ax2+bx+c=0，N：cx2+bx+a=0，其中a×c≠0，a≠c；以下列四个结论中错误的是（ ）
| A． | 如果方程M有两个不相等的实数根，那么方程N也有两个不相等的实数根 | |
| B． | 如果方程M有两根符号相同，那么方程N的两根符号也相同 | |
| C． | 如果5是方程M的一个根，那么$\frac{1}{5}$是方程N的一个根 | |
| D． | 如果方程M和方程N有一个相同的根，那么这个根必是x=1 |
己知a，b，c在数轴上的位置如图所示．