题目内容
16.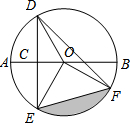 如图,AB是⊙O的直径,弦DE⊥AB,C为垂足,弦DF与AB相交于点P,连接EF,EO,若AC=1,DE=2$\sqrt{3}$,∠EDF=45°,则图中阴影部分的面积( )
如图,AB是⊙O的直径,弦DE⊥AB,C为垂足,弦DF与AB相交于点P,连接EF,EO,若AC=1,DE=2$\sqrt{3}$,∠EDF=45°,则图中阴影部分的面积( )| A. | $\frac{1}{4}π-\frac{1}{2}$ | B. | $\frac{3}{4}π-\frac{3}{2}$ | C. | π | D. | π-2 |
分析 在直角△COE中,利用垂径定理求得半径,再求出扇形的圆心角,再根据扇形面积和三角形的面积公式计算即可.
解答 解:设圆半径是r,则OC=r-2.
∵在直角△COE中,OE=r,CE=$\frac{1}{2}$DE=$\sqrt{3}$,
∴($\sqrt{3}$)2+(r-1)2=r2,
解得r=2.
∵∠EDF=45°,
∴∠EOF=2∠D=90°.
∴S扇形OEF=$\frac{90}{360}$×π×22=π.
∵∠EOF=2∠D=90°,OE=OF=2,
∴SRt△OEF=$\frac{1}{2}$×OE×OF=2.
∴S阴影=S扇形OEF-SRt△OEF=π-2.
故选D.
点评 此题综合考查了垂径定理和解直角三角形及扇形的面积公式.根据已知得出圆的半径是解题关键.

练习册系列答案
相关题目
1.二次函数y=ax2+bx+c图象上部分点的坐标满足如表:
则该函数图象过点( )
| x | … | -3 | -2 | -1 | 0 | 1 | … |
| y | … | -3 | -2 | -3 | -6 | -11 | … |
| A. | (-4,-6) | B. | (-4,-3) | C. | (-5,-2) | D. | (-5,-3) |
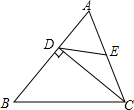 如图,△ABC中,CD⊥AB于点D,若AD=6,DE=5,AC=2DE,则CD的长等于8.
如图,△ABC中,CD⊥AB于点D,若AD=6,DE=5,AC=2DE,则CD的长等于8.