题目内容
7．
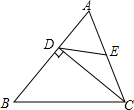如图，△ABC中，CD⊥AB于点D，若AD=6，DE=5，AC=2DE，则CD的长等于8．
分析 先根据直角三角形的性质求出AC的长，再根据勾股定理即可得出结论．
解答 解：∵△ABC中，CD⊥AB于D，
∴∠ADC=90°．
∵E是AC的中点，DE=5，
∴AC=2DE=10．
∵AD=6，
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=8．
故答案为：8．
点评 本题考查的是直角三角形斜边上的中线，熟知在直角三角形中，斜边上的中线等于斜边的一半是解答此题的关键．
练习册系列答案
超能学典应用题题卡系列答案
相关题目
16．
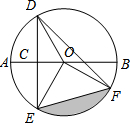如图，AB是⊙O的直径，弦DE⊥AB，C为垂足，弦DF与AB相交于点P，连接EF，EO，若AC=1，DE=2$\sqrt{3}$，∠EDF=45°，则图中阴影部分的面积（ ）
如图，AB是⊙O的直径，弦DE⊥AB，C为垂足，弦DF与AB相交于点P，连接EF，EO，若AC=1，DE=2$\sqrt{3}$，∠EDF=45°，则图中阴影部分的面积（ ）| A． | $\frac{1}{4}π-\frac{1}{2}$ | B． | $\frac{3}{4}π-\frac{3}{2}$ | C． | π | D． | π-2 |