题目内容
在△ABC中,AE平分∠BAC,∠C>∠B.
(1)如图1,若∠C=80°,∠B=50°,求∠AEC的度数;
(2)①如图2,F为AE上的一点,且FD⊥BC于D.试求出∠EFD与∠B、∠C之间的等量关系;
②如图3,当F为AE延长线上的一点时,且FD⊥BC,①中的结论是否仍然成立?(不用说明理由)
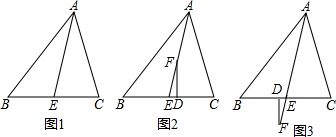
(1)如图1,若∠C=80°,∠B=50°,求∠AEC的度数;
(2)①如图2,F为AE上的一点,且FD⊥BC于D.试求出∠EFD与∠B、∠C之间的等量关系;
②如图3,当F为AE延长线上的一点时,且FD⊥BC,①中的结论是否仍然成立?(不用说明理由)

考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据三角形的内角和定理求出∠BAC,再根据角平分线的定义求出∠BAE,然后根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解;
(2)①根据三角形的内角和定理和角平分线的定义表示出∠BAE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AEC,然后根据直角三角形两锐角互余列式整理即可得解;
②结论仍然成立.
(2)①根据三角形的内角和定理和角平分线的定义表示出∠BAE,再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AEC,然后根据直角三角形两锐角互余列式整理即可得解;
②结论仍然成立.
解答:解:(1)∵∠C=80°,∠B=50°,
∴∠BAC=180°-∠C-∠B=180°-80°-50°=50°,
∵AE平分∠BAC,
∴∠BAE=
∠BAC=
×50°=25°,
由三角形的外角性质得,∠AEC=∠B+∠BAE=50°+25°=75°;
(2)①由三角形的内角和定理得,∠BAC=180°-∠C-∠B,
∵AE平分∠BAC,
∴∠BAE=
∠BAC=
(180°-∠C-∠B),
由三角形的外角性质得,∠AEC=∠B+∠BAE=∠B+
(180°-∠C-∠B)=90°+
(∠B-∠C),
∵FD⊥BC,
∴∠EFD=90°-∠AEC=90°-90°-
(∠B-∠C)=
(∠C-∠B),
即∠EFD=
(∠C-∠B);
②结论∠EFD=
(∠C-∠B)仍然成立.
∴∠BAC=180°-∠C-∠B=180°-80°-50°=50°,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形的外角性质得,∠AEC=∠B+∠BAE=50°+25°=75°;
(2)①由三角形的内角和定理得,∠BAC=180°-∠C-∠B,
∵AE平分∠BAC,
∴∠BAE=
| 1 |
| 2 |
| 1 |
| 2 |
由三角形的外角性质得,∠AEC=∠B+∠BAE=∠B+
| 1 |
| 2 |
| 1 |
| 2 |
∵FD⊥BC,
∴∠EFD=90°-∠AEC=90°-90°-
| 1 |
| 2 |
| 1 |
| 2 |
即∠EFD=
| 1 |
| 2 |
②结论∠EFD=
| 1 |
| 2 |
点评:本题考查了三角形的内角和定理,三角形的一个外角等于与它不相邻的两个内角的和的性质,角平分线的定义,要注意整体思想的利用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
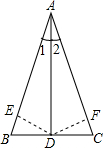 已知在△ABC中,D是BC的中点,∠1=∠2,求证:AB=AC.
已知在△ABC中,D是BC的中点,∠1=∠2,求证:AB=AC.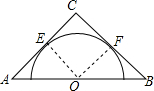 如图所示,在△ABC中,有一半圆内切AC、BC分别于E、F,半圆圆心在AB上,且已知AC=b,BC=a,∠ACB=θ,求半圆的半径.
如图所示,在△ABC中,有一半圆内切AC、BC分别于E、F,半圆圆心在AB上,且已知AC=b,BC=a,∠ACB=θ,求半圆的半径.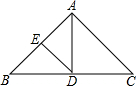 在等腰△ABC中,AB=AC=8,∠B=40°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.求:
在等腰△ABC中,AB=AC=8,∠B=40°,AD是∠BAC的平分线,交BC于D,点E是AB的中点,连接DE.求: