题目内容
已知关于x的一元二次方程x2+4x+m-1=0.
(1)请你为m选取一个合适的整数,使得到的方程有两个相等的实数根;
(2)设x1、x2是 (1)中你所得到的方程的两个实数根,求:
+
的值.
(1)请你为m选取一个合适的整数,使得到的方程有两个相等的实数根;
(2)设x1、x2是 (1)中你所得到的方程的两个实数根,求:
| x2 |
| x1 |
| x1 |
| x2 |
考点:根的判别式,根与系数的关系
专题:
分析:(1)根据一元二次方程根的判别式的意义得到当△=0时,方程有两个相等的实数根,即有42-4(m-1)=0,解得m=5,即m取5;
(2)把m=5代入原方程得到方程整理为x2+4x+4=0,根据根与系数的关系得x1+x2=-4,x1•x2=4,再将
+
变形为两根和与两根积的形式,然后利用整体思想计算即可.
(2)把m=5代入原方程得到方程整理为x2+4x+4=0,根据根与系数的关系得x1+x2=-4,x1•x2=4,再将
| x2 |
| x1 |
| x1 |
| x2 |
解答:解:(1)当△=0时,方程有两个相等的实数根,
即42-4(m-1)=0,解得m=5,
所以m取5;
(2)当m=5时,方程整理为x2+4x+4=0,
则x1+x2=-4,x1•x2=4,
则
+
=
=
=
=2.
即42-4(m-1)=0,解得m=5,
所以m取5;
(2)当m=5时,方程整理为x2+4x+4=0,
则x1+x2=-4,x1•x2=4,
则
| x2 |
| x1 |
| x1 |
| x2 |
| ||||
| x1x2 |
| (x1+x2)2-2x1x2 |
| x1x2 |
| 16-8 |
| 4 |
点评:此题考查一元二次方程根的情况与判别式△的关系:①△>0?方程有两个不相等的实数根;②△=0?方程有两个相等的实数根;③△<0?方程没有实数根.同时考查了一元二次方程的根与系数的关系:x1,x2是方程x2+px+q=0的两根时,x1+x2=-p,x1x2=q.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目
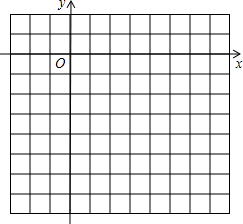 按要求作图并回答问题:
按要求作图并回答问题: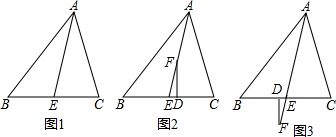
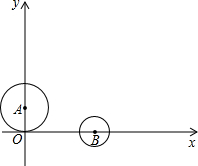 如图,在直角坐标系中A(0,2),B(4,0),已知圆A的半径为2,圆B的半径为1,若圆A固定不动,圆B沿最短路线向圆A靠近使圆A与圆B相外切,求最短路线所在直线的解析式.
如图,在直角坐标系中A(0,2),B(4,0),已知圆A的半径为2,圆B的半径为1,若圆A固定不动,圆B沿最短路线向圆A靠近使圆A与圆B相外切,求最短路线所在直线的解析式.