Question

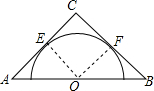如图所示，在△ABC中，有一半圆内切AC、BC分别于E、F，半圆圆心在AB上，且已知AC=b，BC=a，∠ACB=θ，求半圆的半径．

Answer 1

考点：圆的综合题

专题：计算题

分析：连接OE、OF、OC，如图，设⊙O的半径为R，则OE=OF=R，根据切线的性质得OE⊥AC，OF⊥BC，则利用三角形的面积公式得到S_△AOC=

1

2

R•b，S_△BOC=

1

2

R•a，
S_△ABC=

1

2

ab•sinθ，于是利用面积法得到

1

2

R•b+

1

2

R•a=

1

2

ab•sinθ，即可解得R=

ab

a+b

•sinθ．

解答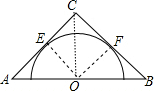：解：连接OE、OF、OC，如图，设⊙O的半径为R，则OE=OF=R，
∵半圆O内切AC、BC分别于E、F，
∴OE⊥AC，OF⊥BC，
∴S_△AOC=

1

2

OE•AC=

1

2

R•b，S_△BOC=

1

2

OF•BC=

1

2

R•a，
∵S_△ABC=

1

2

CA•CB•sin∠ACB=

1

2

ab•sinθ，
∴

1

2

R•b+

1

2

R•a=

1

2

ab•sinθ，
∴R=

ab

a+b

•sinθ．

点评：本题考查了圆的综合题：熟练掌握圆的切线性质；记住三角形的面积公式．