Question

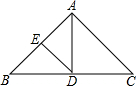在等腰△ABC中，AB=AC=8，∠B=40°，AD是∠BAC的平分线，交BC于D，点E是AB的中点，连接DE．求：
（1）求∠BAD的度数；
（2）求线段DE的长．

Answer 1

考点：等腰三角形的性质,直角三角形斜边上的中线

专题：

分析：（1）根据AD是∠BAC的平分线，利用等腰三角形的性质，得∠BAD=

1

2

∠BAC，即可求解；
（2）根据等腰三角形的三线合一的性质，得到AD是等腰△ABC底边BC上的高，然后根据直角三角形斜边上的中线等于斜边的一半即可求出DE的长．

解答：解：（1）∵AD是∠BAC的平分线，
∴∠BAD=∠CAD，
∵∠BAC=100°，
∴∠BAD=50°；
（2）∵AB=AC，AD平分∠BAC，
∴AD是等腰△ABC底边BC上的高，即∠ADB=90°
在直角三角形ABD中，点E是AB的中点，
∴DE为斜边AB边上的中线，
∴DE=

1

2

AB=4．

点评：本题考查了等腰三角形的性质以及直角三角形斜边上的中线的性质，解题的根据是熟练运用等腰三角形的性质．