题目内容
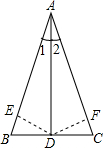已知在△ABC中，D是BC的中点，∠1=∠2，求证：AB=AC．考点：全等三角形的判定与性质
专题：证明题
分析：根据角平分线的性质，可得DE与DF的关系，根据HL，可得△BED与△CFD的关系，根据全等三角形的性质，可得∠B与∠C的关系，根据等腰三角形的判定，可得答案．
解答：证明：∵∠1=∠2，DE⊥AB，DF⊥AC，
∴DE=DF，∠BED=∠CFD=90°．
∵D是BC的中点，
∴BD=CD．
在Rt△BED和Rt△CFD中
，
∴Rt△BED≌Rt△CFD（HL），
∴∠B=∠C，
∴AB=AC．
∴DE=DF，∠BED=∠CFD=90°．
∵D是BC的中点，
∴BD=CD．
在Rt△BED和Rt△CFD中
|
∴Rt△BED≌Rt△CFD（HL），
∴∠B=∠C，
∴AB=AC．
点评：本题考查了全等三角形的判定与性质，利用了角平分线的性质，全等三角形的判定与性质，等腰三角形的判定．
练习册系列答案
相关题目
若两数之和为25，两数之差为23，这两个数是（ ）
| A、24，1 | B、-24，1 |
| C、24，-1 | D、12，13 |
如图，在四边形ABCD中，对角线AC，BD相交于点O，AB∥CD，AO=OC．
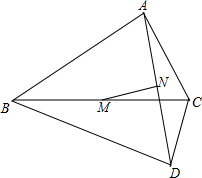如图，在Rt△ABC中，∠BAC=90°，∠ABC=30°，AB=3
按要求作图并回答问题：