题目内容
3.设△ABC是正三角形,点P在△ABC外,且与点A在直线BC异侧,∠BPC=120°,求证:PA=PB+PC.分析 先延长BP至E,使PE=PC,连接CE,证△CPE为等边三角形得CP═PE=CE,再证△ACP≌△BCE得AP=BE,可得PA=PB+PC.
解答 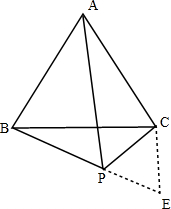 解:如图,延长BP至E,使PE=PC,连接CE,
解:如图,延长BP至E,使PE=PC,连接CE,
∵∠BAC+∠BPC=180°,且∠BAC=60°,
∴∠BPC=120°,
∴∠CPE=60°,又PE=PC,
∴△CPE为等边三角形,
∴CP=PE=CE,∠PCE=60°,
∵△ABC为等边三角形,
∴AC=BC,∠BCA=60°,
∴∠ACB=∠PCE,
∴∠ACB+∠BCP=∠PCE+∠BCP,
即:∠ACP=∠BCE,
∵在△ACP和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACP=∠BCE}\\{PC=PE}\end{array}\right.$,
∴△ACP≌△BCE(SAS),
∴AP=BE,
∵BE=BP+PE,
∴PA=PB+PC.
点评 本题主要考查全等三角形的判定与性质、等边三角形的性质和判定,通过作辅助线构造等边三角形为两三角形全等提供条件是关键.

练习册系列答案
相关题目
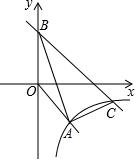 如图,直线y=mx与双曲线y=$\frac{k}{x}$都经过点A(2,-2).
如图,直线y=mx与双曲线y=$\frac{k}{x}$都经过点A(2,-2). 已知:如图,D是△ABC的边BC上的一点,且AB=BD=AD=DC,求∠B,∠C,∠BAC,∠DAC的度数.
已知:如图,D是△ABC的边BC上的一点,且AB=BD=AD=DC,求∠B,∠C,∠BAC,∠DAC的度数. 如图,在△ABC中,AD是角平分线,∠B=60°,∠C=40°.求∠DAC和∠ADB的度数.
如图,在△ABC中,AD是角平分线,∠B=60°,∠C=40°.求∠DAC和∠ADB的度数.