题目内容
8. 如图,在△ABC中,AD是角平分线,∠B=60°,∠C=40°.求∠DAC和∠ADB的度数.
如图,在△ABC中,AD是角平分线,∠B=60°,∠C=40°.求∠DAC和∠ADB的度数.
分析 先根据三角形内角和定理求出∠BAC的度数,再根据角平分线的性质即可得出∠CAD,再根据三角形外角性质,求得∠ADB.
解答 解:∵在△ABC中,∠B=60°,∠C=40°,
∴∠BAC=180°-∠B-∠C=180°-60°-40°=80°,
∵AD是△ABC的角平分线,
∴∠CAD=$\frac{1}{2}$∠BAC=$\frac{1}{2}$×80°=40°,
∵∠ADB是△ACD的外角,
∴∠ADB=∠CAD+∠C=40°+40°=80°.
点评 本题主要考查了三角形内角和定理以及三角形外角性质的运用,解题时注意:三角形内角和是180°,三角形的一个外角等于和它不相邻的两个内角的和.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.下列各组中的两项是同类项的是( )
| A. | 16zy2和-12y2z | B. | -m2n和mn2 | C. | -x2和3x | D. | 0.5a和0.5b |
13. 某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数直方图.如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )
某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数直方图.如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )
 某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数直方图.如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )
某班有48位同学,在一次数学检测中,分数只取整数,统计其成绩,绘制出频数直方图.如图所示,从左到右的小长方形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是( )| A. | 9 | B. | 18 | C. | 12 | D. | 6 |
18.下列各组线段中,成比例的是( )
| A. | a=3 cm,b=5 cm,c=14 cm,d=8cm | B. | a=6 cm,b=8 cm,c=3 cm,d=4cm | ||
| C. | a=3 cm,b=5 cm,c=9 cm,d=12cm | D. | a=2 cm,b=3 cm,c=6cm,d=12cm |
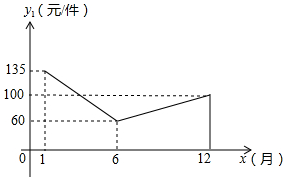 某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=$\left\{\begin{array}{l}{-10x+100(1≤x<6,且x为整数)}\\{\frac{14}{3}x(6≤x≤12,且x为整数)}\end{array}\right.$,月销售量y3(件)与销售月份x(月)满足y3=-10x+20.
某商场在1月至12月份经销某种品牌的服装,由于受到时令的影响,该种服装的销售情况如下:销售价格y1(元/件)与销售月份x(月)的关系大致满足如图的函数,销售成本y2(元/件)与销售月份x(月)满足y2=$\left\{\begin{array}{l}{-10x+100(1≤x<6,且x为整数)}\\{\frac{14}{3}x(6≤x≤12,且x为整数)}\end{array}\right.$,月销售量y3(件)与销售月份x(月)满足y3=-10x+20.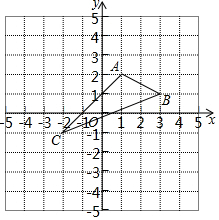 如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).
如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(-2,-1).