题目内容
20.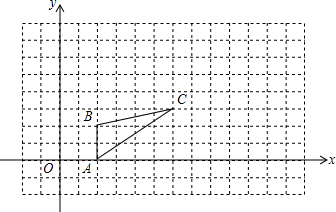 如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).
如图,图中的小方格都是边长为1的正方形,△ABC的A、B、C三点坐标为A(2,0)、B(2,2)、C(6,3).(1)请在图中画出一个△A′B′C′,使△A′B′C′与△ABC是以坐标原点为位似中心,相似比为2的位似图形.
(2)求△A′B′C′的面积.
分析 (1)首先由位似图形的性质,求得A′(4,0),B′(4,4),C′(12,6),继而画出图形;
(2)结合图形,可求得△A′B′C′的底与高,则可求得答案.
解答 解:(1)∵A(2,0)、B(2,2)、C(6,3),△A′B′C′与△ABC是以坐标原点为位似中心,相似比为2的位似图形,
∴A′(4,0),B′(4,4),C′(12,6),如图:
(2)S△A′B′C′=$\frac{1}{2}$×4×8=16.
点评 此题考查了位似变换.注意掌握位似图形的性质是解此题的关键.

练习册系列答案
相关题目
8.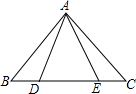 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )| A. | △ABD和△ACE成轴对称 | B. | △ABD和△ACE成中心对称 | ||
| C. | △ABD经过旋转可以和△ACE重合 | D. | △ABD经过平移可以和△ACE重合 |
5.礼堂第一排有m个座位,后面每排比前一排多一个座位,则第n排的座位个数有( )
| A. | m+n | B. | mn+1 | C. | m+(n-1) | D. | n+(n+1) |
 如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的概率是$\frac{5}{7}$.
如图,在3×3的正方形网格中,已有两个小正方形被涂黑.再将图中其余小正方形任意涂黑一个,使整个图案构成一个轴对称图形的概率是$\frac{5}{7}$.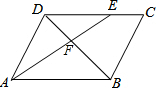 如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.
如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.