题目内容
18.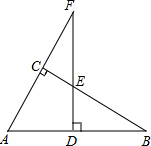 如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.
如图,在△ABC中,∠ACB=90°,点F在边AC的延长线上,且FD⊥AB,垂足为点D,如果AD=6,AB=10,ED=2,那么FD=12.
分析 根据垂直的定义得到∠BDE=∠ADF=90°,根据三角形的内角和得到∠F=∠B,推出△ADF∽△BDE,根据相似三角形的性质得到$\frac{AD}{DE}=\frac{DF}{BD}$,代入数据即可得到结论.
解答 解:∵FD⊥AB,
∴∠BDE=∠ADF=90°,
∵∠ACB=90°,∠CEF=∠BED,
∴∠F=∠B,
∴△ADF∽△BDE,
∴$\frac{AD}{DE}=\frac{DF}{BD}$,
即$\frac{6}{2}=\frac{DF}{10-6}$,
解得:DF=12,
故答案为:12.
点评 本题考查了直角三角形的性质,相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
8.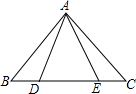 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
 如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )
如图,点D,E在△ABC的边BC上,∠ADE=∠AED,∠BAD=∠CAE.则下列结论正确的是( )| A. | △ABD和△ACE成轴对称 | B. | △ABD和△ACE成中心对称 | ||
| C. | △ABD经过旋转可以和△ACE重合 | D. | △ABD经过平移可以和△ACE重合 |
3.已知等式3a=5b-1,则下列等式中不一定成立的是( )
| A. | 3a-3=5b-4 | B. | 3a+b=6b-1 | C. | 3ac=5bc-1 | D. | b=$\frac{3a+1}{5}$ |
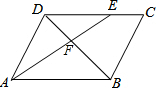 如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$.
如图,在?ABCD中,AB=6,AD=4,∠BAD的平分线AE分别交BD、CD于F、E,那么$\frac{DF}{BF}$=$\frac{2}{3}$. 我国南宋数学家杨辉所著的《详解九章算术》一书中用如图解释了二项和的乘方规律,这个图给出了(a+b)n(其中n=1,2,3,4,…)的展开式的系数规律,请根据这个规律写出(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
我国南宋数学家杨辉所著的《详解九章算术》一书中用如图解释了二项和的乘方规律,这个图给出了(a+b)n(其中n=1,2,3,4,…)的展开式的系数规律,请根据这个规律写出(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
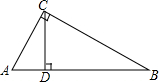 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.