题目内容
15.在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,那么BC的长为( )| A. | m•tanα•cosα | B. | m•cotα•cosα | C. | $\frac{m•tanα}{cosα}$ | D. | $\frac{m•tanα}{sinα}$ |
分析 根据在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,可以用含m和α的三角函数值表示出CD,通过角相等,它们的三角函数值也相等,可以解答本题.
解答 解:∵在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,
∴tanα=$\frac{CD}{AD}=\frac{CD}{m}$,
∴CD=m•tanα,
∵∠ACB=∠A+∠B=90°,∠BDC=∠B+∠BCD=90°,∠A=α,
∴∠BCD=α,
∴cos∠BCD=$\frac{CD}{BC}=\frac{m•tanα}{BC}$,
即cos$α=\frac{m•tanα}{BC}$,
BC=$\frac{m•tanα}{cosα}$.
故选C.
点评 本题考查解直角三角函数,解题的关键是明确各个三角函数值的意义,利用转化的思想找到所求问题需要的条件.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
5.礼堂第一排有m个座位,后面每排比前一排多一个座位,则第n排的座位个数有( )
| A. | m+n | B. | mn+1 | C. | m+(n-1) | D. | n+(n+1) |
3.已知等式3a=5b-1,则下列等式中不一定成立的是( )
| A. | 3a-3=5b-4 | B. | 3a+b=6b-1 | C. | 3ac=5bc-1 | D. | b=$\frac{3a+1}{5}$ |
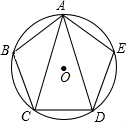 如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)
如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)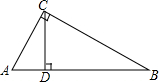 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,CD=3,BD=6,求∠ACD的各个三角函数值. 如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8.
如图,△ABC中,∠ABC=2∠C,AP和BQ分别为∠BAC和∠ABC的角平分线,若△ABQ的周长为20,BP=4,则AB的长为8. 已知:如图,E是AC上一点,AB∥CD,∠B=∠CED,BC=ED.
已知:如图,E是AC上一点,AB∥CD,∠B=∠CED,BC=ED.