题目内容
12.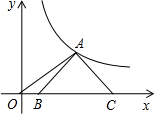 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).
分析 过点A作AD⊥x轴于点D,设点A的坐标为(m,$\frac{3}{m}$)(m>0).由等腰直角三角形的性质可得出BD=AD,再根据线段间的关系可得出OD=OB+BD,从而得出关于m的分式方程,解方程求出m值,代入A点的坐标,此题得解.
解答 解:过点A作AD⊥x轴于点D,如图所示.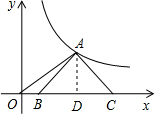
设点A的坐标为(m,$\frac{3}{m}$)(m>0).
∵△ABC为等腰直角三角形,
∴BD=AD=$\frac{3}{m}$,
∴OD=OB+BD=2+$\frac{3}{m}$=m,
解得:m=3,或m=-1(舍去),
经验证m是方程2+$\frac{3}{m}$=m的解.
∴点A的坐标为(3,1).
故答案为:(3,1).
点评 本题考查了等腰直角三角形的性质、反比例函数图象上点的坐标特征以及解分式方程,解题的关键是找出2+$\frac{3}{m}$=m.本题属于基础题,难度不大,解决该题型题目时,根据线段间的关系找出关于m的分式方程是关键.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
3.若$\sqrt{{a}^{2}}$=($\sqrt{a}$)2,则a的取值范围是( )
| A. | a>0 | B. | a≥0 | C. | a=0 | D. | a<0 |
17.若两正整数a和b的最大公因子为405,则下列哪一个数不是a和b的公因子?( )
| A. | 45 | B. | 75 | C. | 81 | D. | 135 |
4.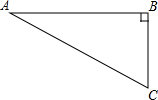 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
2.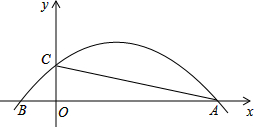 如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
 如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )| A. | (4,3) | B. | (5,$\frac{35}{12}$) | C. | (4,$\frac{35}{12}$) | D. | (5,3) |
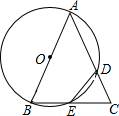 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.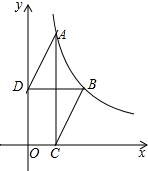 如图,函数y=$\frac{k}{x}(x>0)$的图象经过点A,B,点B的坐标为(1,1),过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,连接AD,BC.若AD∥BC,则线段BC的长度为$\frac{\sqrt{5}}{2}$.
如图,函数y=$\frac{k}{x}(x>0)$的图象经过点A,B,点B的坐标为(1,1),过点A作AC⊥x轴,垂足为C,过点B作BD⊥y轴,垂足为D,连接AD,BC.若AD∥BC,则线段BC的长度为$\frac{\sqrt{5}}{2}$.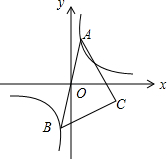 如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.
如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.