题目内容
9.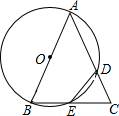 已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.(1)求证:AB=AC;
(2)若AB=4,BC=2$\sqrt{3}$,求CD的长.
分析 (1)由等腰三角形的性质得到∠EDC=∠C,由圆内接四边形的性质得到∠EDC=∠B,由此推得∠B=∠C,由等腰三角形的判定即可证得结论;
(2)连接AE,由AB为直径,可证得AE⊥BC,由(1)知AB=AC,证明△CDE∽△CBA后即可求得CD的长.
解答  (1)证明:∵ED=EC,
(1)证明:∵ED=EC,
∴∠EDC=∠C,
∵∠EDC=∠B,
∴∠B=∠C,
∴AB=AC;
(2)方法一:
解:连接AE,
∵AB为直径,
∴AE⊥BC,
由(1)知AB=AC,
∴BE=CE=$\frac{1}{2}$BC=$\sqrt{3}$,
∵△CDE∽△CBA,
∴$\frac{CD}{CB}=\frac{CE}{AC}$,
∴CE•CB=CD•CA,AC=AB=4,
∴$\sqrt{3}$•2$\sqrt{3}$=4CD,
∴CD=$\frac{3}{2}$.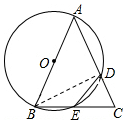 方法二:
方法二:
解:连接BD,
∵AB为直径,
∴BD⊥AC,
设CD=a,
由(1)知AC=AB=4,
则AD=4-a,
在Rt△ABD中,由勾股定理可得:
BD2=AB2-AD2=42-(4-a)2
在Rt△CBD中,由勾股定理可得:
BD2=BC2-CD2=(2$\sqrt{3}$)2-a2
∴42-(4-a)2=(2$\sqrt{3}$)2-a2
整理得:a=$\frac{3}{2}$,
即:CD=$\frac{3}{2}$.
点评 本题考查了圆周角定理,等腰三角形的判定和性质,勾股定理,正确的作出辅助线是解题的关键.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
17.下列事件中,属于必然事件的是( )
| A. | 抛掷1个均匀的骰子,出现4点向上 | |
| B. | 任意数的绝对值都是正数 | |
| C. | 两直线被第三条直线所截,内错角相等 | |
| D. | 13人中至少有2人的生日在同一个月 |
4. 为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
 为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )| A. | 2和1 | B. | 1.25和1 | C. | 1和1 | D. | 1和1.25 |
14.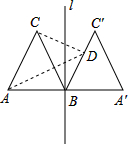 如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
 如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )
如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )| A. | 4 | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2+$\sqrt{3}$ |
 如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.
如图:点C是AE的中点,∠A=∠ECD,AB=CD,求证:∠B=∠D.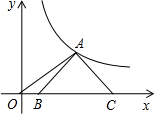 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).