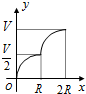题目内容
4.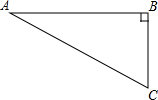 如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )
如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( )| A. | $\frac{\sqrt{3}}{12}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
分析 设BC=x,由含30°角的直角三角形的性质得出AC=2BC=2x,求出AB=$\sqrt{3}$BC=$\sqrt{3}$x,根据题意得出AD=BC=x,AE=DE=AB=$\sqrt{3}$x,作EM⊥AD于M,由等腰三角形的性质得出AM=$\frac{1}{2}$AD=$\frac{1}{2}$x,在Rt△AEM中,由三角函数的定义即可得出结果.
解答 解:如图所示: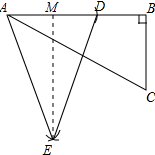 设BC=x,
设BC=x,
∵在Rt△ABC中,∠B=90°,∠A=30°,
∴AC=2BC=2x,AB=$\sqrt{3}$BC=$\sqrt{3}$x,
根据题意得:AD=BC=x,AE=DE=AB=$\sqrt{3}$x,
作EM⊥AD于M,则AM=$\frac{1}{2}$AD=$\frac{1}{2}$x,
在Rt△AEM中,cos∠EAD=$\frac{AM}{AE}$=$\frac{\frac{1}{2}x}{\sqrt{3}x}$=$\frac{\sqrt{3}}{6}$;
故选:B.
点评 本题考查了解直角三角形、含30°角的直角三角形的性质、等腰三角形的性质、三角函数;通过作辅助线求出AM是解决问题的关键.

练习册系列答案
相关题目
19.某场音乐会贩卖的座位分成一楼与二楼两个区域.若一楼售出与未售出的座位数比为4:3,二楼售出与未售出的座位数比为3:2,且此场音乐会一、二楼未售出的座位数相等,则此场音乐会售出与未售出的座位数比为何?( )
| A. | 2:1 | B. | 7:5 | C. | 17:12 | D. | 24:17 |
14.给出一种运算:对于函数y=xn,规定y′=nxn-1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是( )
| A. | x1=4,x2=-4 | B. | x1=2,x2=-2 | C. | x1=x2=0 | D. | x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$ |
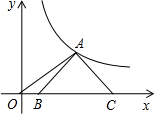 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).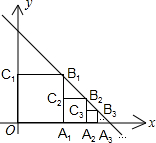 正方形OA1B1C1、A1A2B2C2、A2A3B3C3┅按如图放置,其中点A1、A2、A3┅在x轴的正半轴上,点B1、B2、B3┅在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0),则点An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).
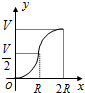
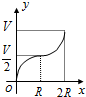
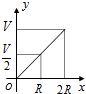
正方形OA1B1C1、A1A2B2C2、A2A3B3C3┅按如图放置,其中点A1、A2、A3┅在x轴的正半轴上,点B1、B2、B3┅在直线y=-x+2上,则点A3的坐标为($\frac{7}{4}$,0),则点An的坐标为($\frac{{2}^{n}-1}{{2}^{n-1}}$,0).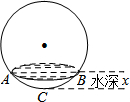 如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )