题目内容
7.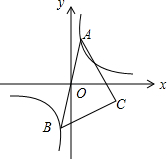 如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.
如图,已知点A是双曲线y=$\frac{4}{x}$在第一象限的分支上的一个动点,连结AO并延长交另一分支于点B,以AB为斜边作等腰直角△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k<0)上运动,则k的值是-4.
分析 连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥x轴于点F,由正比例函数和反比例函数的对称性可得知点O为线段AB的中点,再由等腰直角三角形的性质可得出OC=OA,从而可得出△AOE≌△COF,根据全等三角形的性质结合反比例函数系数k的几何意义即可得出关于k的含绝对值符号的一元一次方程,解方程即可求出k值.
解答 解:连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥x轴于点F,如图所示.
∵线段AB过原点O,且反比例函数图象关于原点对称,
∴点O为线段AB的中点.
∵△ACB为等腰直角三角形,
∴OC⊥AB,OC=OA.
∵∠AOE+∠AOF=90°,∠COF+∠AOF=90°,
∴∠AOE=∠COF.
在△AOE和△COF中,有$\left\{\begin{array}{l}{∠AEO=∠CFO=90°}\\{∠AOE=∠COF}\\{AO=CO}\end{array}\right.$,
∴△AOE≌△COF,
∴S△AOE=S△COF.
∵点A在反比例函数y=$\frac{4}{x}$的图象上,点C在反比例函数y=$\frac{k}{x}$的图象上,
∴有$\frac{1}{2}$×4=$\frac{1}{2}$|k|,
解得:k=±4.
∴点C在第四象限,
∴k=-4.
故答案为:-4.
点评 本题考查了反比例函数系数k的几何意义、等腰直角三角形的性质以及全等三角形的判定及性质,解题的关键是得出$\frac{1}{2}$×4=$\frac{1}{2}$|k|.本题属于中档题,难度不大,解决该题型题目时,根据三角形面积间的关系结合反比例函数系数k的几何意义得出关于k的方程是关键.

练习册系列答案
相关题目
4. 为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
 为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )
为响应“书香校响园”建设的号召,在全校形成良好的阅读氛围,随机调查了部分学生平均每天阅读时间,统计结果如图所示,则本次调查中阅读时间为的众数和中位数分别是( )| A. | 2和1 | B. | 1.25和1 | C. | 1和1 | D. | 1和1.25 |
19.某场音乐会贩卖的座位分成一楼与二楼两个区域.若一楼售出与未售出的座位数比为4:3,二楼售出与未售出的座位数比为3:2,且此场音乐会一、二楼未售出的座位数相等,则此场音乐会售出与未售出的座位数比为何?( )
| A. | 2:1 | B. | 7:5 | C. | 17:12 | D. | 24:17 |
17.下列计算正确的是( )
| A. | (x4)3=x12 | B. | a2•a5=a10 | C. | (3a)2=6a2 | D. | a6÷a2=a3 |
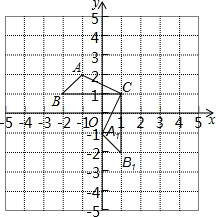 已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(-1,2)、B(-2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(-1,2)、B(-2,1)、C(1,1)(正方形网格中每个小正方形的边长是1个单位长度).
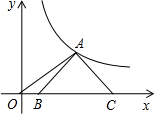 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).