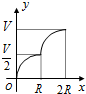题目内容
2.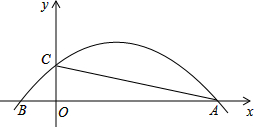 如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )
如图,抛物线y=-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$与x轴交于A,B两点,与y轴交于点C.若点P是线段AC上方的抛物线上一动点,当△ACP的面积取得最大值时,点P的坐标是( )| A. | (4,3) | B. | (5,$\frac{35}{12}$) | C. | (4,$\frac{35}{12}$) | D. | (5,3) |
分析 连接PC、PO、PA,设点P坐标(m,-$\frac{1}{12}{m}^{2}+\frac{2}{3}m+\frac{5}{3}$),根据S△PAC=S△PCO+S△POA-S△AOC构建二次函数,利用函数性质即可解决问题.
解答 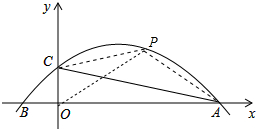 解:连接PC、PO、PA,设点P坐标(m,-$\frac{1}{12}{m}^{2}+\frac{2}{3}m+\frac{5}{3}$)
解:连接PC、PO、PA,设点P坐标(m,-$\frac{1}{12}{m}^{2}+\frac{2}{3}m+\frac{5}{3}$)
令x=0,则y=$\frac{5}{3}$,点C坐标(0,$\frac{5}{3}$),
令y=0则-$\frac{1}{12}$x2+$\frac{2}{3}$x+$\frac{5}{3}$=0,解得x=-2或10,
∴点A坐标(10,0),点B坐标(-2,0),
∴S△PAC=S△PCO+S△POA-S△AOC=$\frac{1}{2}$×$\frac{5}{3}$×m+$\frac{1}{2}$×10×(-$\frac{1}{12}{m}^{2}+\frac{2}{3}m+\frac{5}{3}$)-$\frac{1}{2}$×$\frac{5}{3}$×10=-$\frac{5}{12}$(m-5)2+$\frac{125}{12}$,
∴x=5时,△PAC面积最大值为$\frac{125}{12}$,
此时点P坐标(5,$\frac{35}{12}$).
故点P坐标为(5,$\frac{35}{12}$).
点评 本题考查二次函数的性质、抛物线与x轴交点,解题的关键是构建二次函数,利用二次函数性质解决问题,属于中考常考题型.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
17.下列计算正确的是( )
| A. | (x4)3=x12 | B. | a2•a5=a10 | C. | (3a)2=6a2 | D. | a6÷a2=a3 |
14.给出一种运算:对于函数y=xn,规定y′=nxn-1.例如:若函数y=x4,则有y′=4x3.已知函数y=x3,则方程y′=12的解是( )
| A. | x1=4,x2=-4 | B. | x1=2,x2=-2 | C. | x1=x2=0 | D. | x1=2$\sqrt{3}$,x2=-2$\sqrt{3}$ |
11.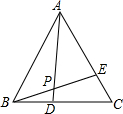 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
 如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )
如图:等边三角形ABC中,BD=CE,AD与BE相交于点P,则∠APE的度数是( )| A. | 45° | B. | 55° | C. | 60° | D. | 75° |
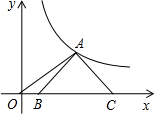 如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1).
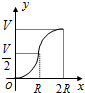
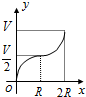
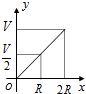
如图,等腰Rt△ABC的斜边BC在x轴上,顶点A在反比例函数$y=\frac{3}{x}(x>0)$的图象上,连接OA,若OB=2,则点A的坐标为(3,1). 如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )