题目内容
17.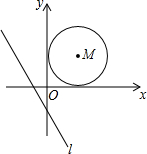 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(2,2)为圆心,2个单位长度为半径的⊙M以每秒1个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为$\frac{13±2\sqrt{13}}{3}$秒.
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(2,2)为圆心,2个单位长度为半径的⊙M以每秒1个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为$\frac{13±2\sqrt{13}}{3}$秒.
分析 根据题意确定直线的相对速度,作出直线与圆相切时的图形,求出AM、AE,证明△ADM∽△AEC,△ADM∽△AFG得到成比例线段,求出时间.
解答 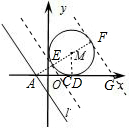 解:∵直线以每秒3个单位的速度向右平移,⊙M以每秒1个单位长度的速度向右平移,
解:∵直线以每秒3个单位的速度向右平移,⊙M以每秒1个单位长度的速度向右平移,
∴相当于⊙M静止,直线以每秒2个单位的速度向右平移,
直线y=-$\frac{4}{3}$x-$\frac{4}{3}$与x轴的交点A的坐标为(-1,0),
由题意可知,⊙M的半径为2,
在直角三角形AMD中,AD=3,DM=2,
由勾股定理得,AM=$\sqrt{13}$,AE=$\sqrt{13}$-2,
当直线l与⊙M相切于E时,
△ADM∽△AEC,
AC:AM=AE:AD,
即AC:$\sqrt{13}$=($\sqrt{13}$-2):3,
解得AC=$\frac{13-2\sqrt{13}}{3}$,
∴当t=$\frac{13-2\sqrt{13}}{3}$s时,直线l与⊙M相切;
当直线l与⊙M相切于点F时,
△ADM∽△AFG,
AG:AM=AF:AD,
即AG:$\sqrt{13}$=($\sqrt{13}$+2):3,
解得:AG=$\frac{13+2\sqrt{13}}{3}$,
∴当t=$\frac{13+2\sqrt{13}}{3}$时,直线l与⊙M相切,
故答案为:$\frac{13±2\sqrt{13}}{3}$.
点评 本题考查的是直线与圆的关系,通过分析得到直线的相对速度是解题的关键,解答时,注意运用分情况讨论的思想,正确运用相似三角形的性质也是重点.

练习册系列答案
相关题目
8.下列图形都是由同样大小的黑色三角形按一定规律所组成的,其中第①个图形中一共有 4 个黑色三角形,第②个图形中一共有 8 个黑色三角形,第③个图形中一共有13 个黑色三角形,…,按此规律排列下去,第⑦个图形中黑色三角形的个数是( )


| A. | 65 | B. | 53 | C. | 43 | D. | 34 |
9.下列运算中正确的是( )
| A. | 3a-a=3 | B. | a2•a3=a6 | C. | (-2a)3=-6a 3 | D. | ab2÷a=b 2 |
6.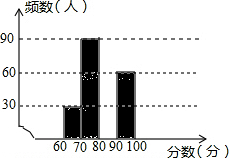 2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.
2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.
请你根据表中提供的信息,解答下列问题:
(1)此次调查的样本容量为300;
(2)在表中:m=120,n=0.30;
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,那么请你估计该校学生笔试成绩的优秀人数大约是1200名.
 2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.
2017年6月5日是第46个“世界环境日”,为提高学生的环保意识,某校组织该校2000名学生参加了“环保知识”竞赛,为了解“环保知识”的笔试情况,学校随机抽取了部分参赛同学的成绩,整理并绘制成如图所示的不完整的图表.| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
(1)此次调查的样本容量为300;
(2)在表中:m=120,n=0.30;
(3)补全频数分布直方图;
(4)如果比赛成绩80分以上(含80分)为优秀,那么请你估计该校学生笔试成绩的优秀人数大约是1200名.
7.要使分式$\frac{3}{x-2}$有意义,则x的取值范围是( )
| A. | x≠-2 | B. | x>2 | C. | x<2 | D. | x≠2 |
 如图,直线y=x+2与抛物线y=$\frac{1}{4}{x}^{2}$+c相交于A、B两点,若∠AOB=45°,则c的值为$\frac{\sqrt{11}}{2}$.
如图,直线y=x+2与抛物线y=$\frac{1}{4}{x}^{2}$+c相交于A、B两点,若∠AOB=45°,则c的值为$\frac{\sqrt{11}}{2}$.