题目内容
5.已知函数y=$\frac{1}{3}$x+1的图象与x轴、y轴分别相交于点A、B.点C的坐标为(2,0).(1)求直线BC的函数解析式.
(2)点E是直线AB上的一个点,且△AEC是直角三角形.求点E的坐标.
分析 (1)求出B的坐标,设直线BC的解析式为y=kx+b,把B、C的坐标代入求出k、b即可;
(2)分为两种情况:当∠ACE=90°和∠AEC=90°,求出E的坐标即可.
解答 解:(1)当x=0时,y=1,
所以B的坐标为(0,1),
设直线BC的解析式为y=kx+b,
把B、C的坐标代入得:$\left\{\begin{array}{l}{b=1}\\{0=2k+b}\end{array}\right.$,
解得:k=-0.5,b=1,
所以直线BC的函数解析式为y=-0.5x+1;
(2)分为两种情况:①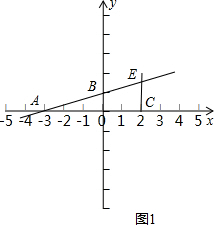
当∠ACE=90°时,把x=2代入y=$\frac{1}{3}$x+1得:y=$\frac{5}{3}$,
此时E的坐标为(2,$\frac{5}{3}$);
②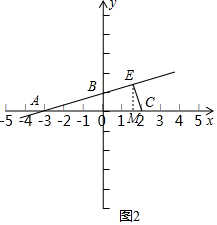
当∠AEC=90°时,CE⊥AB,
∵直线AB的解析式是y=$\frac{1}{3}$x+1,
∴设直线CE的解析式是y=-3x+b,
把(2,0)代入得:b=6,
∴直线CE的解析式是y=-3x+6,
解方程组$\left\{\begin{array}{l}{y=\frac{1}{3}x+1}\\{y=-3x+6}\end{array}\right.$得:$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=\frac{3}{2}}\end{array}\right.$,
即E的坐标为($\frac{3}{2}$,$\frac{3}{2}$).
点评 本题考查了用待定系数法求出一次函数的解析式,能之前运用待定系数法求函数的解析式是解此题的关键.

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | 2x2•6x4=12x8 | B. | 4a2-a2=3 | C. | (x+y)2=x2+y2 | D. | (y4)m÷(y3)m=ym |
13.下列说法错误的是( )
| A. | 若a=b,则a+c=b+c | B. | 若a=b,则a-c=b-c | C. | 若a=b,则ac=bc | D. | 若a=b,则$\frac{a}{c}$=$\frac{b}{c}$ |
15.某校为了备战2018体育中考,因此在八年级抽取了50名女学生进行“一分钟仰卧起坐”测试,测试的情况绘制成表格如下:
(1)通过计算算得出这50名女学生进行“一分钟仰卧起坐”的平均数是30,请写出这50名女学生进行“一分钟仰卧起坐”的众数和中位数,它们分别是28、28.
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
| 个数 | 16 | 22 | 25 | 28 | 29 | 30 | 35 | 37 | 40 | 42 | 45 | 46 |
| 人数 | 2 | 1 | 7 | 18 | 1 | 9 | 5 | 2 | 1 | 1 | 1 | 2 |
(2)学校根据测试数据规定八年级女学生“一分钟仰卧起坐”的合格标准为28次,已知该校五年级有女生250名,试估计该校五年级女生“一分钟仰卧起坐”的合格人数是多少?
 如图是一个由4个相同的长方体组成的立体图形,它的左视图是( )
如图是一个由4个相同的长方体组成的立体图形,它的左视图是( )



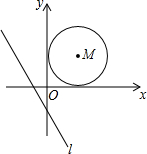 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(2,2)为圆心,2个单位长度为半径的⊙M以每秒1个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为$\frac{13±2\sqrt{13}}{3}$秒.
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(2,2)为圆心,2个单位长度为半径的⊙M以每秒1个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为$\frac{13±2\sqrt{13}}{3}$秒.