题目内容
10.在菱形ABCD中,∠A=60°,其所对的对角线长为4,则菱形ABCD的面积是8$\sqrt{3}$.分析 直接利用菱形的性质结合勾股定理得出菱形的另一条对角线的长,进而利用菱形面积求法得出答案.
解答 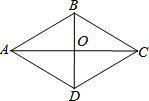 解:如图所示:
解:如图所示:
∵在菱形ABCD中,∠BAD=60°,其所对的对角线长为4,
∴可得AD=AB,故△ABD是等边三角形,
则AB=AD=4,
故BO=DO=2,
则AO=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,故AC=4$\sqrt{3}$,
则菱形ABCD的面积是:$\frac{1}{2}$×4×4$\sqrt{3}$=8$\sqrt{3}$.
故答案为:8$\sqrt{3}$.
点评 此题主要考查了菱形的性质以及勾股定理,正确得出菱形的另一条对角线的长是解题关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
5.下列哪一个选项中的等式成立( )
| A. | $\sqrt{{2}^{2}}$=2 | B. | $\sqrt{{3}^{3}}$=3 | C. | $\sqrt{{4}^{4}}$=4 | D. | $\sqrt{{5}^{5}}$=5 |
15.已知∠A与∠B互为补角,则∠A+∠B=( )
| A. | 180° | B. | 100° | C. | 90o | D. | 45° |
16.下列运算正确的是( )
| A. | 2x2•6x4=12x8 | B. | 4a2-a2=3 | C. | (x+y)2=x2+y2 | D. | (y4)m÷(y3)m=ym |
 如图,直线AB,CD交于点O,OA平分∠EOC,∠EOC:∠EOD=4:5,则∠BOD=40度.
如图,直线AB,CD交于点O,OA平分∠EOC,∠EOC:∠EOD=4:5,则∠BOD=40度.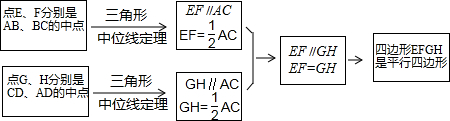
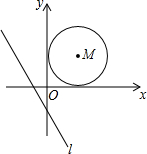 如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(2,2)为圆心,2个单位长度为半径的⊙M以每秒1个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为$\frac{13±2\sqrt{13}}{3}$秒.
如图,已知直线l:y=-$\frac{4}{3}$x-$\frac{4}{3}$以每秒3个单位的速度向右平移;同时以点M(2,2)为圆心,2个单位长度为半径的⊙M以每秒1个单位长度的速度向右平移,当直线l与⊙M相切时,则它们运动的时间为$\frac{13±2\sqrt{13}}{3}$秒.