题目内容
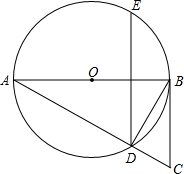
AB是⊙O的直径,直线CD切⊙O于点C,AC平分∠DAB.
(1)求证:AD⊥CD;
(2)若AC=2,AD=
,求⊙O的半径.
(1)求证:AD⊥CD;
(2)若AC=2,AD=
| 3 |
考点:切线的性质
专题:
分析:(1)连接OC,由题意得OC⊥CD.又因为AC平分∠DAB,则∠1=∠2=
∠DAB.即可得出AD∥OC,则AD⊥CD;
(2)连接BC,则∠ACB=90°,可证明△ADC∽△ACB.则
=
,从而求得R.
| 1 |
| 2 |
(2)连接BC,则∠ACB=90°,可证明△ADC∽△ACB.则
| AD |
| AC |
| AC |
| 2R |
解答: (1)证明:连接OC,
(1)证明:连接OC,
∵直线CD与⊙O相切于C点,AB是⊙O的直径,
∴OC⊥CD.
又∵AC平分∠DAB,
∴∠1=∠2=
∠DAB.
又∵∠COB=2∠1=∠DAB,
∴AD∥OC,
∴AD⊥CD.
(2)解:连接BC,则∠ACB=90°,
在△ADC和△ACB中,∵∠1=∠2,∠3=∠ACB=90°,
∴△ADC∽△ACB.
∴
=
∴R=
=
 (1)证明:连接OC,
(1)证明:连接OC,∵直线CD与⊙O相切于C点,AB是⊙O的直径,
∴OC⊥CD.
又∵AC平分∠DAB,
∴∠1=∠2=
| 1 |
| 2 |
又∵∠COB=2∠1=∠DAB,
∴AD∥OC,
∴AD⊥CD.
(2)解:连接BC,则∠ACB=90°,
在△ADC和△ACB中,∵∠1=∠2,∠3=∠ACB=90°,
∴△ADC∽△ACB.
∴
| AD |
| AC |
| AC |
| 2R |
∴R=
| AC2 |
| 2AD |
2
| ||
| 3 |
点评:本题考查了切线的性质、圆周角定理以及相似三角形的判定和性质,是中档题,难度不大.

练习册系列答案
相关题目
 如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连接BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )
如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连接BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )| A、DE⊥AB |
| B、∠EDB=28° |
| C、∠ADE=∠ABD |
| D、OB=BC |
 作出这段弧的圆心O.
作出这段弧的圆心O.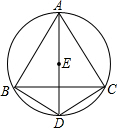 如图,四边形ABDC是圆内接四边形,E是AD上一点,且是△ABC的内心.求证:DB=DE=DC.
如图,四边形ABDC是圆内接四边形,E是AD上一点,且是△ABC的内心.求证:DB=DE=DC. 如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是
如图,一张半径为1的圆形纸片在边长为a(a≥3)的正方形内任意移动,则在该正方形内,这张圆形纸片“不能接触到的部分”的面积是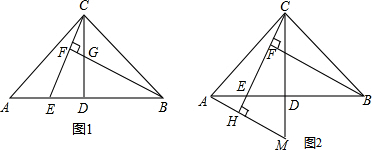
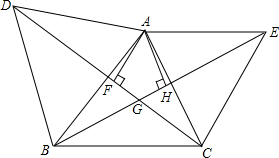 如图,已知△ABD、△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H.
如图,已知△ABD、△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H.