Question

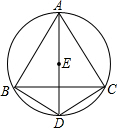如图，四边形ABDC是圆内接四边形，E是AD上一点，且是△ABC的内心．求证：DB=DE=DC．

Answer 1

考点：三角形的内切圆与内心

专题：证明题

分析：连结BE，如图，根据三角形内心的性质得到AD平分∠BAC，BE平分∠ABC，则∠2=∠CAD，∠3=∠4，根据圆周角定理得

BD

=

CD

，所以BD=CD，∠5=∠2，再利用三角形外角性质得∠1=∠2+∠3，则∠1=∠5+∠4，即∠1=∠DBE，根据等腰三角形的性质得DB=DE，于是得到DB=DE=DC．

解答：证明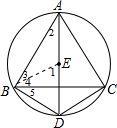：连结BE，如图，
∵E是AD上一点，且是△ABC的内心，
∴AD平分∠BAC，BE平分∠ABC，
∴∠2=∠CAD，∠3=∠4，
∴

BD

=

CD

，
∴BD=CD，∠5=∠2，
∵∠1=∠2+∠3，
∴∠1=∠5+∠4，即∠1=∠DBE，
∴DB=DE，
∴DB=DE=DC．

点评：本题考查了三角形的内切圆与内心：与三角形各边都相切的圆叫三角形的内切圆，三角形的内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．三角形的内心就是三角形三个内角角平分线的交点．也考查了圆周角定理．