题目内容
某商品现在的售价为每件50元,每周可卖出400件.市场调查反映:如调整价格,涨价1元,每周要少卖出10件.已知该商品的进价为每件30元,设每件涨价x元.
(1)为尽可能让利于顾客并使每周利润为8750元,求x;
(2)写出每周销售利润y(单位:元)与x之间的函数解析式;
(3)当售价定为多少元时,会获得每周销售最大利润?并求出每周最大销售利润.
(1)为尽可能让利于顾客并使每周利润为8750元,求x;
(2)写出每周销售利润y(单位:元)与x之间的函数解析式;
(3)当售价定为多少元时,会获得每周销售最大利润?并求出每周最大销售利润.
考点:二次函数的应用
专题:
分析:(1)根据题意列出方程,即可解决问题.
(2)直接列出函数关系式,即可结局问题.
(3)运用二次函数的性质,求出最大值,即可解决问题.
(2)直接列出函数关系式,即可结局问题.
(3)运用二次函数的性质,求出最大值,即可解决问题.
解答:解:(1)由题意得:(50+x-30)(400-10x)=8750,
整理得:x2-20x+75=0,
解得:x=15或5,
故为尽可能让利于顾客并使每周利润为8750元,取x的值为5.
(2)由题意得:
y=(50+x-30)(400-10x)
=-10x2+200x+8000,
即y=-10x2+200x+8000,
(3)∵-10<0,
∴当x=-
=10时,y取得最大值,
此时y=-1000+2000+8000=9000(元),
即当售价为60元时,会获得每周销售最大利润,每周最大销售利润为9000元.
整理得:x2-20x+75=0,
解得:x=15或5,
故为尽可能让利于顾客并使每周利润为8750元,取x的值为5.
(2)由题意得:
y=(50+x-30)(400-10x)
=-10x2+200x+8000,
即y=-10x2+200x+8000,
(3)∵-10<0,
∴当x=-
| 200 |
| 2×(-10) |
此时y=-1000+2000+8000=9000(元),
即当售价为60元时,会获得每周销售最大利润,每周最大销售利润为9000元.
点评:该题主要考查了二次函数的性质及其应用问题;解题的关键是深入把握题意,准确找出命题中隐含的数量关系,正确列出函数关系式来分析、解答.

练习册系列答案
相关题目
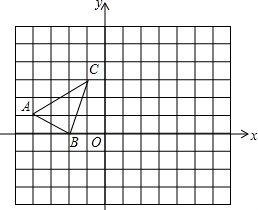 如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-2,0),点C的坐标为(-1,3).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(-4,1),点B的坐标为(-2,0),点C的坐标为(-1,3).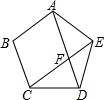 如图,正五边形ABCDE中,对角线AD、CE相交于F,求证:
如图,正五边形ABCDE中,对角线AD、CE相交于F,求证: 如图,等边ABC的边长为3.D,E分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,求AF的长度.
如图,等边ABC的边长为3.D,E分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,求AF的长度. 如图,OA=2,OB=4,∠AOB=90°,点C为直线AB上一动点,以BC为腰作等腰直角三角形△BCE,过A、C、E三点作⊙O1,EF⊥BE交⊙O1于F点.
如图,OA=2,OB=4,∠AOB=90°,点C为直线AB上一动点,以BC为腰作等腰直角三角形△BCE,过A、C、E三点作⊙O1,EF⊥BE交⊙O1于F点. 如图,在Rt△ABC中,∠BAC=90°,∠BAC的平分线交BC于点O,以O为圆心做圆,⊙O与AC相切于点D.
如图,在Rt△ABC中,∠BAC=90°,∠BAC的平分线交BC于点O,以O为圆心做圆,⊙O与AC相切于点D.