题目内容
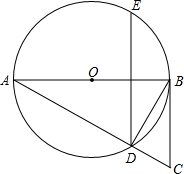 如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连接BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )
如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连接BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )| A、DE⊥AB |
| B、∠EDB=28° |
| C、∠ADE=∠ABD |
| D、OB=BC |
考点:切线的判定
专题:
分析:利用切线的判定方法,结合平行线的性质以及圆周角定理得出∠ABC=90°即可.
解答:解:A、∵DE⊥AB,DE∥CB,
∴∠ABC=90°,
∵AB为直径,
∴BC是⊙O的切线,故此选项错误;
B、∵∠EDB=28°,以AB为直径的⊙O交AC于点D,
∴∠BDE+∠ADE=90°,
∵∠BAD=28°,
∴∠BAD+∠ADE=90°,
∴DE⊥AB,
∵DE∥CB,
∴∠ABC=90°,
∵AB为直径,
∴BC是⊙O的切线,故此选项错误;
C、∵以AB为直径的⊙O交AC于点D,
∴∠BDE+∠ADE=90°,
∵∠ADE=∠ABD,
∴∠BDE+∠ABD=90°,
∴DE⊥AB,
∵DE∥CB,
∴∠ABC=90°,
∵AB为直径,
∴BC是⊙O的切线,故此选项错误;
D、OB=BC,无法得出,AB⊥BC,故符合题意.
故选:D.
∴∠ABC=90°,
∵AB为直径,

∴BC是⊙O的切线,故此选项错误;
B、∵∠EDB=28°,以AB为直径的⊙O交AC于点D,
∴∠BDE+∠ADE=90°,
∵∠BAD=28°,
∴∠BAD+∠ADE=90°,
∴DE⊥AB,
∵DE∥CB,
∴∠ABC=90°,
∵AB为直径,
∴BC是⊙O的切线,故此选项错误;
C、∵以AB为直径的⊙O交AC于点D,
∴∠BDE+∠ADE=90°,
∵∠ADE=∠ABD,
∴∠BDE+∠ABD=90°,
∴DE⊥AB,
∵DE∥CB,
∴∠ABC=90°,
∵AB为直径,
∴BC是⊙O的切线,故此选项错误;
D、OB=BC,无法得出,AB⊥BC,故符合题意.
故选:D.
点评:此题主要考查了切线的判定以及圆周角定理和平行线的性质等知识,正确应用圆周角定理是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,OA=2,OB=4,∠AOB=90°,点C为直线AB上一动点,以BC为腰作等腰直角三角形△BCE,过A、C、E三点作⊙O1,EF⊥BE交⊙O1于F点.
如图,OA=2,OB=4,∠AOB=90°,点C为直线AB上一动点,以BC为腰作等腰直角三角形△BCE,过A、C、E三点作⊙O1,EF⊥BE交⊙O1于F点.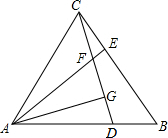 如图,等边△ABC中,D,E分别为AB,BC边上的点,且BD=CE,AE与CD交于点F,AG⊥CD于点G.
如图,等边△ABC中,D,E分别为AB,BC边上的点,且BD=CE,AE与CD交于点F,AG⊥CD于点G. 如图,△ABC中,点A的坐标为(0,-2),点C的坐标为(2,1),点B的坐标为(3,-1),要使△ACD与△ACB全等,那么符合条件的点D有
如图,△ABC中,点A的坐标为(0,-2),点C的坐标为(2,1),点B的坐标为(3,-1),要使△ACD与△ACB全等,那么符合条件的点D有 已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数y=
已知A(n,-2),B(1,4)是一次函数 y=kx+b的图象和反比例函数y=