题目内容
13. 如图,己知AB⊥AD,BD⊥DC,BD是AB、BC的比例中项,求证:BD平分∠ABC.
如图,己知AB⊥AD,BD⊥DC,BD是AB、BC的比例中项,求证:BD平分∠ABC.
分析 要证明BD平分∠ABC,只要证明∠ABD=∠DBC即可,根据题目中的条件可以证明Rt△BAD∽Rt△BDC,从而可以解答本题.
解答 证明:∵AB⊥AD,BD⊥DC,
∴∠BAD=∠BDC=90°,
∵BD是AB、BC的比例中项,
∴$\frac{AB}{BD}=\frac{BD}{BC}$,
∴Rt△BAD∽Rt△BDC,
∴∠ABD=∠DBC,
∴BD平分∠ABC.
点评 本题考查比例线段、三角形相似,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.$\sqrt{(a-b)^{2}}$+$\root{5}{(a-b)^{5}}$的值是( )
| A. | 0 | B. | 2(a-b) | C. | 0或2(a-b) | D. | a-b |
4. 已知抛物线y=ax2+bx+c如图所示,则关于x的方程ax2+bx+c=0的根的情况是( )
已知抛物线y=ax2+bx+c如图所示,则关于x的方程ax2+bx+c=0的根的情况是( )
 已知抛物线y=ax2+bx+c如图所示,则关于x的方程ax2+bx+c=0的根的情况是( )
已知抛物线y=ax2+bx+c如图所示,则关于x的方程ax2+bx+c=0的根的情况是( )| A. | 有两个相等的实数根 | B. | 有两个不相等的正实根 | ||
| C. | 有两个异号实数根 | D. | 没有实数根 |
1.下列四个命题中,真命题是( )
| A. | 长度相等的两条弧是等弧 | |
| B. | 相等的弧所对的圆心角相等 | |
| C. | 在同圆或等圆中,相等的弦所对的弧相等 | |
| D. | 圆是轴对称图形,圆的每一条直径都是对称轴 |
8.等腰三角形的两边长为1和3,则周长为( )
| A. | 7 | B. | 5 | C. | 7或5 | D. | 无法确定 |
18.已知关于x的一元二次方程(a-1)x2-2x+1=0无实数根,则a的取值范围是( )
| A. | a<2 | B. | a>2 | C. | a<-2 | D. | a<2且a≠1 |
2.已知m是方程x2-3x+1=0的根,则代数式m4-21m+10的值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.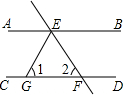 如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=50°,则∠1的度数是( )
如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=50°,则∠1的度数是( )
 如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=50°,则∠1的度数是( )
如图,已知AB∥CD,直线EF分别交AB,CD于点E、F,EG平分∠AEF,若∠2=50°,则∠1的度数是( )| A. | 70° | B. | 65° | C. | 60° | D. | 50° |