题目内容
18.已知关于x的一元二次方程(a-1)x2-2x+1=0无实数根,则a的取值范围是( )| A. | a<2 | B. | a>2 | C. | a<-2 | D. | a<2且a≠1 |
分析 根据一元二次方程的定义结合根的判别式即可得出关于a的一元一次不等式组,解不等式组即可得出结论.
解答 解:∵关于x的一元二次方程(a-1)x2-2x+1=0无实数根,
∴$\left\{\begin{array}{l}{a-1≠0}\\{△=(-2)^{2}-4(a-1)<0}\end{array}\right.$,
解得:a>2.
故选B.
点评 本题考查了根的判别式以及解一元一次不等式组,根据根的判别式结合一元二次方程的定义找出关于a的一元一次不等式组是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.下列各式中,$\frac{3}{x+2}$,$\frac{x+2}{3}$,$\frac{{x}^{2}-{y}^{3}}{4}$,$\frac{5x-1}{4x+1}$,分式的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.在-|-2|、|-(+2)|、3-π、-(-4)、(-1)2n(n为正整数)中负数有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
3.对于抛物线y=-2(x-5)2+3,下列说法正确的是( )
| A. | 开口向下,顶点坐标(5,3) | B. | 开口向上,顶点坐标(5,3) | ||
| C. | 开口向下,顶点坐标(-5,3) | D. | 开口向上,顶点坐标(-5,3) |
10.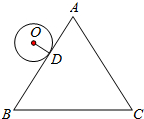 如图,等边△ABC的周长为16π,半径是2的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
如图,等边△ABC的周长为16π,半径是2的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
 如图,等边△ABC的周长为16π,半径是2的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )
如图,等边△ABC的周长为16π,半径是2的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )| A. | 3周 | B. | 4周 | C. | 5周 | D. | 6周 |
7.如果两个有理数的和为零,那么这两个有理数( )
| A. | 互为相反数 | B. | 互为倒数 | C. | 有一个等于零 | D. | 无法确定 |
8.如图,能正确描述A到B到C的变换的是( )


| A. | A旋转135°后平移2cm,再平移2cm | B. | A旋转135°后平移4cm,再平移4cm | ||
| C. | A平移2cm后旋转135°,再平移2cm | D. | A平移2cm后旋转135°,再平移4cm |
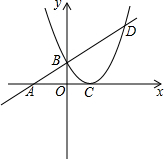 如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次图象交于y轴上的一点B,二次函数的顶点C在x轴上,且OC=2.
如图,已知一次函数y=0.5x+2的图象与x轴交于点A,与二次图象交于y轴上的一点B,二次函数的顶点C在x轴上,且OC=2. 如图,己知AB⊥AD,BD⊥DC,BD是AB、BC的比例中项,求证:BD平分∠ABC.
如图,己知AB⊥AD,BD⊥DC,BD是AB、BC的比例中项,求证:BD平分∠ABC.