题目内容
8.等腰三角形的两边长为1和3,则周长为( )| A. | 7 | B. | 5 | C. | 7或5 | D. | 无法确定 |
分析 因为等腰三角形的两边为1和3,但已知中没有点明底边和腰,所以有两种情况,需要分类讨论,还要注意利用三角形三边关系考查各情况能否构成三角形.
解答 解:当1为底时,其它两边都为3,1、3、3可以构成三角形,周长为7;
当1为腰时,其它两边为1和3,
∵1+1=2<3,
所以不能构成三角形,故舍去,
∴周长为7.
故选A.
点评 本题考查了等腰三角形的性质;对于底和腰不等的等腰三角形,若条件中没有明确哪边是底哪边是腰时,应在符合三角形三边关系的前提下分类讨论.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
19.实数-8,-3,-5,0中最小的数是( )
| A. | 0 | B. | -8 | C. | -5 | D. | -3 |
3.若2m=3n,则下列比例式中不正确的是( )
| A. | $\frac{m}{n}=\frac{3}{2}$ | B. | $\frac{m}{3}=\frac{n}{2}$ | C. | $\frac{m}{2}=\frac{n}{3}$ | D. | $\frac{2}{n}=\frac{3}{m}$ |
20.下列计算中,正确的是( )
| A. | -(-2)2=4 | B. | -[-(5)]=5 | C. | $\frac{2^2}{3}=\frac{4}{9}$ | D. | ${({-3})^2}×({-\frac{1}{3}})=3$ |
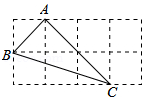 如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( )
如图的2×4的正方形网格中,△ABC的顶点都在小正方形的格点上,这样的三角形称为格点三角形,在网格中与△ABC成轴对称的格点三角形一共有( ) 如图,己知AB⊥AD,BD⊥DC,BD是AB、BC的比例中项,求证:BD平分∠ABC.
如图,己知AB⊥AD,BD⊥DC,BD是AB、BC的比例中项,求证:BD平分∠ABC.
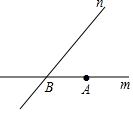 如图,直线m,n交于点B,m、n的夹角为50°,点A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的C点有多少个?( )
如图,直线m,n交于点B,m、n的夹角为50°,点A是直线m上的点,在直线n上寻找一点C,使△ABC是等腰三角形,这样的C点有多少个?( )