题目内容
5.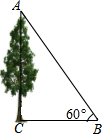 有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
分析 根据题意可知BC⊥AC,在Rt△ABC中,BC=a,∠ABC=60°,利用三角函数即可求出树的高度AC.
解答 解:∵BC⊥AC,BC=a,∠ABC=60°,
∴tan∠ABC=$\frac{AC}{BC}$,
∴AC=BC•tan60°=$\sqrt{3}$a.
答:树的高度AC为$\sqrt{3}$a.
点评 本题考查了解直角三角形的应用,关键是根据仰角构造直角三角形,利用三角函数求解.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
1.(1)填表:
(2)在同一直角坐标系中,作出上述三个函数的图象;
(3)它们三者的图象有什么异同?它们的开口方向、对称轴、顶点坐标分别是多少?
(4)由抛物线y=-2x2怎样平移得到抛物线y=-2x2+1与y=-2x2-1?
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y=-2x2 | |||||||
| y=-2x2+1 | |||||||
| y=-2x2-1 |
(3)它们三者的图象有什么异同?它们的开口方向、对称轴、顶点坐标分别是多少?
(4)由抛物线y=-2x2怎样平移得到抛物线y=-2x2+1与y=-2x2-1?

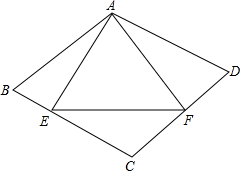 如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为点E、F,连接EF.
如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为点E、F,连接EF.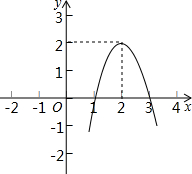 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题: