题目内容
1.(1)填表:| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y=-2x2 | |||||||
| y=-2x2+1 | |||||||
| y=-2x2-1 |
(3)它们三者的图象有什么异同?它们的开口方向、对称轴、顶点坐标分别是多少?
(4)由抛物线y=-2x2怎样平移得到抛物线y=-2x2+1与y=-2x2-1?
分析 (1)直接计算填表即可;
(2)利用描点法可画出这三个函数的图象;
(3)分别由图象可得出开口方向、对称轴及顶点坐标;
(4)利用平移的规律得出答案即可.
解答 解:(1)填表:
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y=-2x2 | -8 | -2 | 0 | -2 | -8 | ||
| y=-2x2+1 | -7 | -1 | 1 | -1 | -7 | ||
| y=-2x2-1 | -9 | -3 | -1 | -3 | -9 |

(3)它们三者的图象开口大小、方向相同,顶点坐标不同;
y=-2x2的开口方向向下、对称轴y轴、顶点坐标是(0,0);
y=-2x2+1的开口方向向下、对称轴y轴、顶点坐标是(0,1);
y=-2x2-1的开口方向向下、对称轴y轴、顶点坐标是(0,-1);
(4)由抛物线y=-2x2向上平移1个单位得到抛物线y=-2x2+1,向下平移1个单位得到y=-2x2-1.
点评 本题主要考查函数图象的画法及二次函数的图象的性质,掌握基本的描点法作函数图象是解题的关键.

练习册系列答案
相关题目
14.将一个正方形桌面砍去一个角后得到的桌面是( )
| A. | 五边形 | B. | 四边形 | C. | 三边形 | D. | 以上都有可能 |
10.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 5cm,6cm,10cm | C. | 1cm,1cm,3cm | D. | 3cm,4cm,9cm |
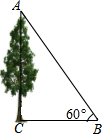 有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗? 如图,△ABC的角平分线交于点O.
如图,△ABC的角平分线交于点O.