题目内容
15.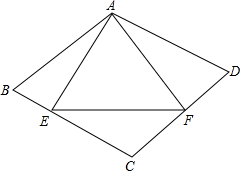 如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为点E、F,连接EF.
如图,在菱形ABCD中,AB=4,∠B=60°,AE⊥BC,AF⊥CD,垂足分别为点E、F,连接EF.(1)求证:△ABE≌△ADF;
(2)求△AEF的面积.
分析 (1)由菱形的性质得出AB=AD=BC=CD,∠B=∠D,由AAS证明△ABE≌△ADF即可;
(2)由全等三角形的性质得出AE=AF,证明△AEF是等边三角形,再由三角函数求出出AE、EF,过A作AM⊥EF于M,利用三角函数求出AM,即可求出△AEF的面积.
解答 (1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AB=AD=BC=CD,∠B=∠D=60°,
∵AE⊥BC,AF⊥CD,
∴∠AEB=∠AFD=90°,
在△ABE和△ADF中,$\left\{\begin{array}{l}{∠B=∠D}&{\;}\\{∠AEB=∠AFD}&{\;}\\{AB=AD}&{\;}\\{\;}&{\;}\end{array}\right.$,
∴△ABE≌△ADF(AAS);
(2)解:∵△ABE≌△ADF,
∴AE=AF,
∵∠B=60°,
∴∠BAD=120°,∠BAE=30°,
∴∠EAF=120°-30°-30°=60°,
∴△AEF是等边三角形,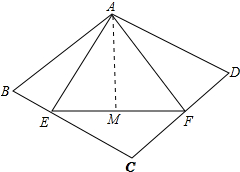
∴∠AEF=60°,
∵AB=4,
∴BE=$\frac{1}{2}$AB=2,
∴AE=2$\sqrt{3}$,
∴EF=AE=2$\sqrt{3}$,
过A作AM⊥EF于M,如图所示:
则AM=AE•sin60°=2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=3,
∴△AEF的面积=$\frac{1}{2}$EF•AM=$\frac{1}{2}$×2$\sqrt{3}$×3=3$\sqrt{3}$.
点评 此题考查了菱形的性质、全等三角形的判定与性质、等边三角形的判定与性质、三角函数;熟练掌握菱形的性质,并能进行推理论证与计算是解决问题的关键.

练习册系列答案
相关题目
7.线段AB=3,且AB∥x轴,若A(-2,4),则将线段向下平移4个单位长度后,点B的对应点的坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (-5,1) | D. | (1,0)或(-5,0) |
4.下列是二元一次方程的是( )
| A. | 3x=10 | B. | 2x2=y | C. | y+$\frac{1}{x}$=2 | D. | x+8y=0 |
10.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 5cm,6cm,10cm | C. | 1cm,1cm,3cm | D. | 3cm,4cm,9cm |
 表示(其中,n≥1).这是用无理数表示有理数的一个范例.
表示(其中,n≥1).这是用无理数表示有理数的一个范例.
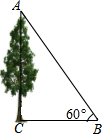 有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?