题目内容
14.点A从数轴上表示+5的位置开始移动,第一次沿数轴先向右移动1个单位长度,再向左移动2个单位长度到达A1点;第二次从点A1开始,沿数轴先向右移动3个单位长度,再向左移动4个单位长度到达点A2;第三次从点A2开始,沿数轴向右移动5个单位长度,再向左移动6个单位长度到达点A3…(1)数轴上点A1表示的数是+4;
(2)数轴上点A5表示的数是0;
(3)数轴上点8表示的数是-3.
分析 根据数轴上的点的坐标向右为加,向左为减的特点可分别求出第一次、第二次、第三次移动后这个点在数轴上表示的数,找出规律即可求出第n次移动结果这个点在数轴上表示的数.
解答 解:(1)∵点A从数轴上表示+5的A点开始移动,第一次先向右移动1个单位,再向左移动2个单位,
∴第一次移动后这个点在数轴上表示的数为5+1-2=4;
(2)同理可得,第二次移动后这个数在数轴上表示的点为4+1-2=3;
第三次移动后这个数在数轴上表示的点为3+1-2=2;
第四次移动后这个数在数轴上表示的点为2+1-2=1;
第五次移动后这个数在数轴上表示的点为1+1-2=0.
(3)这个点移动后的点的坐标可知,这个点每移动一次点的坐标减少1,
则第n次移动结果这个点在数轴上表示的数为5-n,
依题意有5-n=-3,
解得n=8.
故数轴上点8表示的数是-3.
故答案为:4,0,8.
点评 此题考查了数轴,解答此题的关键是先求出前五次这个点移动后在数轴上表示的数,再根据此数值找出规律即可解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.线段AB=3,且AB∥x轴,若A(-2,4),则将线段向下平移4个单位长度后,点B的对应点的坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (-5,1) | D. | (1,0)或(-5,0) |
19.下列各等式成立的是( )
| A. | $\frac{n}{n-m}$=-$\frac{n}{m+n}$ | B. | $\frac{n}{m-n}$=-$\frac{n}{m+n}$ | C. | $\frac{n}{n-m}$=-$\frac{-n}{m+n}$ | D. | $\frac{n}{n-m}$=-$\frac{n}{m-n}$ |
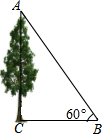 有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗? 如图,△ABC的角平分线交于点O.
如图,△ABC的角平分线交于点O. 如图,两个四边形是轴对称图形.
如图,两个四边形是轴对称图形.