题目内容
17.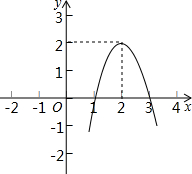 二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c<0的解集;
(3)写出y随x的增大而增大的自变量x的取值范围;
(4)若方程ax2+bx+c=k没有实数根,求k取值范围.
分析 (1)找到抛物线与x轴的交点即可得出方程ax2+bx+c=0的两个根;
(2)找出抛物线在x轴下方时x的取值范围即可;
(3)结合图形可写出y随x的增大而减小的自变量x的取值范围;
(4)根据图象可以看出k取值范围.
解答 解:(1)由图象可得:x1=1,x2=3;
(2)结合图象可得:x<1或x>3时,y<0,
即当x<1或x>3时,ax2+bx+c<0;
(3)根据图象可得当x≥2时,y随x的增大而减小;
(4)根据图象可得,k>2时,方程ax2+bx+c=k没有实数根.
点评 本题主要考查了二次函数的图象与方程和不等式的关系,求方程ax2+bx+c=0的两个根即为抛物线与x轴的交点的横坐标;判断y>0,y=0,y<0时,x的取值范围,要结合开口方向,图象与x轴的交点而定;判断函数的增减性,要结合开口方向,对称轴而定;方程ax2+bx+c=k有无实数根,看顶点坐标的纵坐标即可.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
10.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 5cm,6cm,10cm | C. | 1cm,1cm,3cm | D. | 3cm,4cm,9cm |
 如图,直角△ABC绕着C点按逆时针方向旋转到△DEC位置.那么点∠A的对应角是:∠CDE.
如图,直角△ABC绕着C点按逆时针方向旋转到△DEC位置.那么点∠A的对应角是:∠CDE.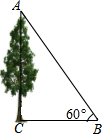 有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗? 如图,△ABC的角平分线交于点O.
如图,△ABC的角平分线交于点O. 如图,两个四边形是轴对称图形.
如图,两个四边形是轴对称图形.