题目内容
19.用同样大小黑色棋子按如图所示的规律摆放:
(1)第6个图形有多少颗黑色棋子?
(2)第670个图形有多少个棋子?
(3)2014个棋子能摆放成这样的图形吗?为什么?
分析 (1)第1个图形有6个棋子;第2个图形有9个棋子;第3个图形有12个棋子;第4个图形有15个棋子;第5个图形有18个棋子;第六个图形则有21个棋子;
(2)根据图中所给的黑色棋子的颗数,找出其中的规律,根据规律列出式子,即可求出答案;
(3)解方程即可解答.
解答 解:(1)由图形可以看出:第1个图形有6个棋子;第2个图形有9个棋子;第3个图形有12个棋子;第4个图形有15个棋子;
所以第5个图形有18个棋子;第六个图形则有21个棋子;
(2)由(1)可以看出第n个图形有3n+3个棋子,所以第670个图形有3×670+3=2013个棋子;
(3)根据题意得
3n+3=2014,
n=$\frac{2011}{3}$,
∵n不是整数,
∴2014个棋子不能摆放成这样的图形.
点评 此题考查了图形的变化类,是一道关于数字猜想的问题,关键是通过归纳与总结,得到其中的规律.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
9.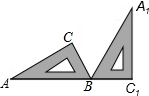 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针方向旋转一个角度到A1B1C1的位置,使得点A,B,C1在同一条直线上,那么这个角度等于( )| A. | 30° | B. | 60° | C. | 90° | D. | 120° |
7.线段AB=3,且AB∥x轴,若A(-2,4),则将线段向下平移4个单位长度后,点B的对应点的坐标为( )
| A. | (1,0) | B. | (0,1) | C. | (-5,1) | D. | (1,0)或(-5,0) |
14.将一个正方形桌面砍去一个角后得到的桌面是( )
| A. | 五边形 | B. | 四边形 | C. | 三边形 | D. | 以上都有可能 |
4.下列是二元一次方程的是( )
| A. | 3x=10 | B. | 2x2=y | C. | y+$\frac{1}{x}$=2 | D. | x+8y=0 |
10.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm,3cm,5cm | B. | 5cm,6cm,10cm | C. | 1cm,1cm,3cm | D. | 3cm,4cm,9cm |
 如图,直角△ABC绕着C点按逆时针方向旋转到△DEC位置.那么点∠A的对应角是:∠CDE.
如图,直角△ABC绕着C点按逆时针方向旋转到△DEC位置.那么点∠A的对应角是:∠CDE.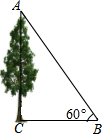 有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗?
有一棵树较高(如图),无法直接量出它的高度,可以先用测角器在离树底部不远处的地面上找一点B,使此时测得树顶A的仰角为60°,再用皮尺测得BC之间的距离为a,由此你能得出这棵树的高度吗? 如图,两个四边形是轴对称图形.
如图,两个四边形是轴对称图形.