题目内容
16.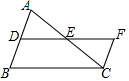 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是DF=AC.
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是DF=AC.
分析 根据三角形中位线和线段中点得出DE=$\frac{1}{2}$BC,AE=$\frac{1}{2}$AC,推出AE=DE,根据旋转的性质得出全等,推出AE=EC,DE=EF,推出AC=DF.
解答 解:∵AC=BC,点D、E分别是边AB、AC的中点,
∴DE=$\frac{1}{2}$BC,AE=$\frac{1}{2}$AC,
∵AC=BC,
∴AE=DE,
∵将△ADE绕点E旋转180°得△CFE,
∴△ADE≌△CFE,
∴AE=CE,DE=EF,
∴AE=CE=DE=EF,
∴AC=DF.
故答案为:DF=AC.
点评 本题主要考查了旋转的性质以及三角形中位线定理的运用,三角形的中位线平行于第三边,并且等于第三边的一半.熟练掌握旋转变换只改变图形的位置,不改变图形的形状与大小是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
5.下列那组数字是勾股数( )
| A. | 7、24、25 | B. | $\frac{3}{4}$,1,$\frac{5}{4}$ | C. | 9、40、42 | D. | 12、15、20 |
7.下列说法错误的是( )
| A. | a2与(-a)2相等 | B. | $\sqrt{{a}^{2}}$与$\sqrt{(-a)^{2}}$互为相反数 | ||
| C. | $\root{3}{a}$与$\root{3}{-a}$是互为相反数 | D. | -|a|与|-a|互为相反数 |
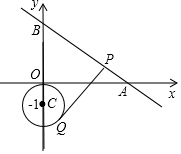 如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点A、B;点Q是以C(0,-2)为圆心、2为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是2$\sqrt{3}$.
如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点A、B;点Q是以C(0,-2)为圆心、2为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是2$\sqrt{3}$.