题目内容
1.设a1=32-12,a2=52-32,…,an=(2n+1)2-(2n-1)2(n为大于0的自然数).(1)探究an是否为6的倍数,并用文字表述出你所获得的结论;
(2)若一个数的算术平方根是一个自然数,则称这个数是“完全平方数”,例如:1,4,9,16,…,是“完全平方数”.试写出a1,a2,a3,…,an,这一列数中从小到大排列的前3个“完全平方数”.
分析 (1)将an的表达式根据平方差公式计算出来,看是否是8的倍数.
(2)由(1)可得$\sqrt{{a}_{n}}$=$\sqrt{8n}$=2$\sqrt{2n}$,根据该式依次列出所需的完全平方数即可.
解答 解:(1)an不是为6的倍数.
理由:根据平方差公式计算an=(2n+1)2-(2n-1)2=(2n+1-2n+1)(2n+1+2n-1)=8n,
故an是8的倍数,不是6的倍数.
这个结论用文字语言表述为:两个连续奇数的平方差是8的倍数.
(2)∵an=8n,
∴$\sqrt{{a}_{n}}$=$\sqrt{8n}$=2$\sqrt{2n}$,
∴当n分别取2、8、18时得到一列数中从小到大排列的前3个“完全平方数”.
n=2时,an=16,
n=8时,an=64,
n=18时,an=144,
∴这一列数中从小到大排列的前3个“完全平方数”为:16、64、144.
点评 此题考查了完全平方数的知识以及平方差公式的应用.注意利用平方差公式求得an=8n是关键.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
10.计算(3a-b)(-3a-b)等于( )
| A. | 9a2-6ab-b2 | B. | b2-6ab-9a2 | C. | b2-9a2 | D. | 9a2-b2 |
6.某礼堂第一排有m个座位,后面每排比前一排多一个座位,则第20排有( )个座位.
| A. | m+21 | B. | m+20 | C. | m+19 | D. | m+18 |
 如图,AD、BC交于点O,EF过点O交AB于点E,交CD于点F,且AO=DO,BO=CO.求证:
如图,AD、BC交于点O,EF过点O交AB于点E,交CD于点F,且AO=DO,BO=CO.求证: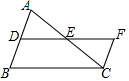 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是DF=AC.
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是DF=AC. 如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是①②③.
如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是①②③.