题目内容
5.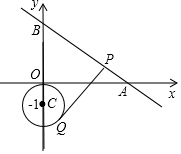 如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点A、B;点Q是以C(0,-2)为圆心、2为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是2$\sqrt{3}$.
如图,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于点A、B;点Q是以C(0,-2)为圆心、2为半径的圆上一动点,过Q点的切线交线段AB于点P,则线段PQ的最小值是2$\sqrt{3}$.
分析 过点C作CP⊥直线AB与点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,由点到直线的距离求出CP的长度,再根据勾股定理即可求出PQ的长度.
解答 解:
过点C作CP⊥直线AB于点P,过点P作⊙C的切线PQ,切点为Q,此时PQ最小,连接CQ,如图所示.
直线AB的解析式为y=-$\frac{3}{4}$x+3y,即3x+4y-12=0,
∴CP=$\frac{|-8-12|}{\sqrt{{3}^{2}+{4}^{2}}}$=4.
∵PQ为⊙C的切线,
∴在Rt△CQP中,CQ=2,∠CQP=90°,
∴PQ=$\sqrt{C{P}^{2}-C{Q}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题主要考查了切线的性质、点到直线的距离以及勾股定理,解题的关键是确定P、Q点的位置.本题属于中档题,难度不大,解决该题型题目时,借助于切线的性质寻找到PQ取最小值时点P、Q的位置是关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 如图,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线MG,MN,NG,三条垂线围成△MNG,求证:△MNG是等边三角形.
如图,过等边△ABC的顶点A,B,C依次作AB,BC,CA的垂线MG,MN,NG,三条垂线围成△MNG,求证:△MNG是等边三角形.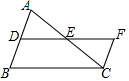 如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是DF=AC.
如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得到△CFE,则DF与AC的数量关系是DF=AC. 如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是①②③.
如图,△ABC中,∠B=90°,AB=11,BC=10,若⊙O的半径为5且与AB、BC相切,以下说法不正确的是①②③. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交与点O,AD与BC交与点P,BE与CD交与点Q,连接PQ.有下列结论:
如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交与点O,AD与BC交与点P,BE与CD交与点Q,连接PQ.有下列结论: 有理数a、b、c在数轴上的位置如图所示,则化简|a+c|+|a-b|-|c-a|=-a-b.
有理数a、b、c在数轴上的位置如图所示,则化简|a+c|+|a-b|-|c-a|=-a-b.