题目内容
因式分解
(1)-2a3+12a2-18a
(2)9a2(x-y)+4b2(y-x);
(3)9(m+n)2-16(m-n)2
(4)m4-16n4
(5)4a2b2-(a2+b2)2
(6)(x+y)2-4(x+y-1)
(1)-2a3+12a2-18a
(2)9a2(x-y)+4b2(y-x);
(3)9(m+n)2-16(m-n)2
(4)m4-16n4
(5)4a2b2-(a2+b2)2
(6)(x+y)2-4(x+y-1)
考点:提公因式法与公式法的综合运用
专题:
分析:(1)首先提公因式-2a,然后利用公式法分解即可;
(2)首先提公因式(x-y),然后利用平方差公式分解;
(3)利用平方差公式即可分解;
(4)利用平方差公式即可分解;
(5)首先利用平方差公式,然后利用完全平方公式即可分解;
(6)把x+y看成一个整体,化简,然后利用公式法分解即可.
(2)首先提公因式(x-y),然后利用平方差公式分解;
(3)利用平方差公式即可分解;
(4)利用平方差公式即可分解;
(5)首先利用平方差公式,然后利用完全平方公式即可分解;
(6)把x+y看成一个整体,化简,然后利用公式法分解即可.
解答:解:(1)原式=-2a(a2-6a+9)=-2a(a-3)2;
(2)原式=(x-y)(9a2-4b2)=(x-y)(3a+2b)(3a-2b);
(3)原式=【(3(m+n)+4(m-n)】【(3(m+n)-4(m-n)】=(7m-n)(7n-m);
(4)原式=(m2+4n2)(m2-4n2)=(m2+4n2)(m+2n)(m-2n);
(5)原式=(2ab+a2+b2)(2ab-a2-b2)=-(a+b)2(a-b)2;
(6)原式=(x+y)2-4(x+y)+4=(x+y-1)2.
(2)原式=(x-y)(9a2-4b2)=(x-y)(3a+2b)(3a-2b);
(3)原式=【(3(m+n)+4(m-n)】【(3(m+n)-4(m-n)】=(7m-n)(7n-m);
(4)原式=(m2+4n2)(m2-4n2)=(m2+4n2)(m+2n)(m-2n);
(5)原式=(2ab+a2+b2)(2ab-a2-b2)=-(a+b)2(a-b)2;
(6)原式=(x+y)2-4(x+y)+4=(x+y-1)2.
点评:本题考查了提公因式法,公式法分解因式,提取公因式后利用完全平方公式进行二次分解,注意分解要彻底.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
平行四边形的一条边长是10cm,那么它的两条对角线的长可能是( )
| A、6cm和8cm |
| B、10cm和20cm |
| C、8cm和12cm |
| D、12cm和32cm |
已知抛物线y=x2+x-2与直线y=5x-m没有公共点,则m的取值范围是( )
| A、m<6 | B、m>6 |
| C、m≤6 | D、m≥2 |
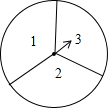 如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.
如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止. 如图,抛物线y=ax2+bx+c分别交坐标轴于A(-2,0)、B(6,0)、C(0,4),则0≤ax2+bx+c<4的解集是
如图,抛物线y=ax2+bx+c分别交坐标轴于A(-2,0)、B(6,0)、C(0,4),则0≤ax2+bx+c<4的解集是