题目内容
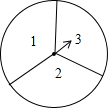 如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.
如图,转盘被平均分成三块扇形,转动转盘,转动过程中,指针保持不动,转盘停止后,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.(1)转动转盘一次,转到数字是3的区域的概率是多少?
(2)转动转盘两次,用画树状图或列表的方法求两次指针所指区域数字不同的概率;
(3)在第(2)题中,两次转到的区域的数字作为两条线段的长度,如果第三条线段的长度为5,求这三条线段能构成三角形的概率.
考点:列表法与树状图法,三角形三边关系
专题:
分析:(1)因为转盘被平均分成三块扇形,所以转动转盘一次,转到数字是3的区域的概率是
;
(2)列表得出所有的可能情况个数,找出数字不同的情况个数,即可求出所求的概率;
(3)根据(2)得到所有情况个数,利用三角形的三边关系判断能构成三角形的个数,即可求出所求的概率.
| 1 |
| 3 |
(2)列表得出所有的可能情况个数,找出数字不同的情况个数,即可求出所求的概率;
(3)根据(2)得到所有情况个数,利用三角形的三边关系判断能构成三角形的个数,即可求出所求的概率.
解答:解:(1)转到数字是3的区域的概率:P=
;
(2)列表如下:
所有可能情况有9种,其中数字不同的情况有6种,
则P数字不同=
=
;
(3)所有的情况有9种,分别为:1,1,5;2,1,5;3,1,5;1,2,5;2,2,5;3,2,5;1,3,5;2,3,5;3,3,5,其中构成三角形的有1种,为3,3,5一种,则P构成三角形=
| 1 |
| 3 |
(2)列表如下:
| 1 | 2 | 3 | |
| 1 | (1,1) | (2,1) | (3,1) |
| 2 | (1,2) | (2,2) | (3,2) |
| 3 | (1,3) | (2,3) | (3,3) |
则P数字不同=
| 6 |
| 9 |
| 2 |
| 3 |
(3)所有的情况有9种,分别为:1,1,5;2,1,5;3,1,5;1,2,5;2,2,5;3,2,5;1,3,5;2,3,5;3,3,5,其中构成三角形的有1种,为3,3,5一种,则P构成三角形=
| 1 |
| 9 |
点评:此题考查了列表法与树状图法,以及概率公式,用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
下列事件是必然事件的是( )
| A、抛掷一枚硬币100次,有50次正面朝上 |
| B、面积相等的两个三角形全等 |
| C、a是实数,|a|>0 |
| D、方程x2-2x-1=0必有实数根 |
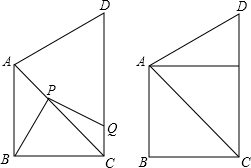 如图,在四边形ABCD中,AB=BC=1,∠ABC=90°,且AB∥CD,将一把三角尺的直角顶点P放在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,探究:
如图,在四边形ABCD中,AB=BC=1,∠ABC=90°,且AB∥CD,将一把三角尺的直角顶点P放在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q,探究: