题目内容
已知△ABC，BE、CF、AD分别是△ABC的三条中线，证明：三条中线交于一点G．
考点：三角形的重心
专题：证明题
分析：延长AG与BC相交于点D′，过点B作BH∥CF交AG的延长线于H，根据三角形的中位线平行于第三边并且等于第三边的一半可得G是AH的中点，再根据三角形的中位线平行于第三边并且等于第三边的一半可得GE∥CH，从而得到四边形BHCG是平行四边形，根据平行四边形对角线互相平分可得BD′=CD′，从而得到点D′与点D重合．
解答：
证明：如图，延长AG与BC相交于点D′，过点B作BH∥CF交AG的延长线于H，
∵CF是△ABC的中线，
∴G是AH的中点，
∵BE是△ABC的中线，
∴GE是△ACH的中位线，
∴GE∥CH，
∴四边形BHCG是平行四边形，
∴BD′=CD′，
∵AD是△ABC的中线，
∴点D′与点D互相重合，
∴AD经过BE、CF的交点G，
即三条中线交于一点G．
证明：如图，延长AG与BC相交于点D′，过点B作BH∥CF交AG的延长线于H，∵CF是△ABC的中线，
∴G是AH的中点，
∵BE是△ABC的中线，
∴GE是△ACH的中位线，
∴GE∥CH，
∴四边形BHCG是平行四边形，
∴BD′=CD′，
∵AD是△ABC的中线，
∴点D′与点D互相重合，
∴AD经过BE、CF的交点G，
即三条中线交于一点G．
点评：本题考查了三角形的重心，三角形的中位线平行于第三边并且等于第三边的一半，平行四边形的判定与性质，作辅助线，考虑利用三角形的中位线定理是解题的关键．
练习册系列答案
出彩同步大试卷系列答案
相关题目
如图，AB=DB，∠1=∠2，请你添加一个适当的条件，使△ABC≌△DBE，请问添加下面哪个条件不能判断△ABC≌△DBE的有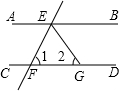
已知：如图，AB∥CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF．若∠2=65°，则∠1=