题目内容
已知抛物线y=x2+x-2与直线y=5x-m没有公共点,则m的取值范围是( )
| A、m<6 | B、m>6 |
| C、m≤6 | D、m≥2 |
考点:二次函数的性质
专题:
分析:把两函数的交点问题转化为一元二次方程根的情况:有两解析式组成方程组,整理得x2-4x+m-2=0,然后根据判别式的意义得△=42-4(m-2)≥0,最后解关于m的不等式即可.
解答:解:根据题意得x2+x-2=5x-m,
整理得x2-4x+m-2=0,
因为抛物线y=x2+x-2与直线y=5x-m没有公共点,
所以△=42-4(m-2)≥0,
解得m≤6.
故选B.
整理得x2-4x+m-2=0,
因为抛物线y=x2+x-2与直线y=5x-m没有公共点,
所以△=42-4(m-2)≥0,
解得m≤6.
故选B.
点评:考查了二次函数的性质,解题的关键是了解能根据直线与抛物线的交点的个数得到有关m的不等式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列各式中不能用平方差公式计算的是( )
| A、(x-y)(x+y) |
| B、(-x-y)(-x+y) |
| C、(-x+y)(x+y) |
| D、(x-y)(y-x) |
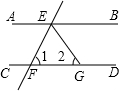 已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠2=65°,则∠1=
已知:如图,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF.若∠2=65°,则∠1=