题目内容
下面计算错误的是（ ）
A. (y-z)(y+z)=y2-z2 B. (m-n)(m+n)=n2-m C. x5·x20 = x25 D. y3 · y5 = y8
B
【解析】根据平方差公式可得：选项A，(y-z)(y+z)=y2-z2；选项B， (m-n)(m+n)=m2-n2；根据同底数幂的乘法法则可得：选项C，x5·x20 = x25；选项D， y3 · y5 = y8.故选B.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
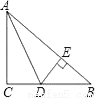
如图，△ABC中，∠C=90°，AD平分∠BAC，交BC于D，若DC=7，则点D到AB的距离DE= ．
7
【解析】试题分析： ∵∠C=90°，AD平分∠BAC，点D到AB的距离DE，∴DE=DC=7．故填7． (c-a2b2)2 等于（ ）
A. c -ab2 B. c2 -2a2b2c+a4b4 C. c-a2b2c+a4b4 D. c2 -2abc+a4b
B
【解析】根据完全平方公式可得：(c-a2b2)2=c2 -2a2b2c+a4b4 ，故选B. 102×98等于_______；
9996
【解析】102×98=（100+2）×（100-2）=10000-4=9996. [c+（a2)2][c-（a2)2]等于（ ）
A. c -a2 B. c2 -a8 C. c2 -a2 D. c2 -a4
B
【解析】根据平方差公式和幂的乘方法则可得：[c+（a2)2][c-（a2)2]= =c2 -a8，故选B. （x+5y）（x-5y）等于（ ）
A. x2-5y 2 B. x2-y 2 C. x2-25y 2 D. 25x2-y 2
C
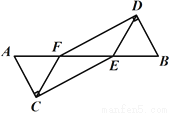
【解析】根据平方差公式可得：（x+5y）（x-5y）=x2-25y 2 ，故选C. 如图， 
四点共线，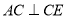 
， 
， 
， 
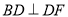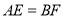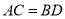.求证：CE∥DF.
证明见解析.
【解析】试题分析：利用HL证明RtΔACE?RtΔBDF，根据全等三角形的性质即可得∠AEC=∠BFD，由内错角相等，两直线平行即可得CE∥DF.
试题解析：
∵AC⊥CE,BD⊥DF，
∴∠ACE=∠BDF=90°，
又∵AE=BF,AC=BD，
∴RtΔACE?RtΔBDF(HL)，
∴∠AEC=∠BFD，
∴CE∥DF.
... 下列航空公司的标志中，是轴对称图形的是（ ）
A. 
B. 
C. 
D. 
C
【解析】A、B、D三个选项中的图形沿着一条直线折叠以后，直线两旁的部分均不能互相重合，只有C选项，沿着图中的一条直线（虚线）折叠，直线两旁的部分均能够互相重合，由此图形是轴对称图形，
故选择C. 下列代数式中，属于分式的是( )
A. －3 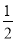B. 
a－b
C.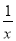 
D. －4a3b
C
【解析】根据整式和分式的定义，即可以对各选项进行判断．
【解析】
A. －3 是整式；
B. a－b是整式；
C. 是分式；
D. －4a3b是整式；
故选C.