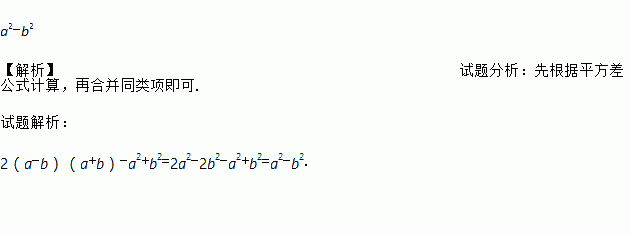题目内容
2(a-b)(a+b)-a2+b2
 a2-b2
【解析】试题分析:先根据平方差公式计算,再合并同类项即可.
试题解析:
2(a-b)(a+b)-a2+b2=2a2-2b2-a2+b2=a2-b2.
a2-b2
【解析】试题分析:先根据平方差公式计算,再合并同类项即可.
试题解析:
2(a-b)(a+b)-a2+b2=2a2-2b2-a2+b2=a2-b2.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )

A. 4 cm B. 2 cm C. 3 cm D. 1 cm
 C
【解析】∵ED⊥AB,∠A=30°,
∴AE=2ED,
∵AE=6cm,
∴ED=3cm.
∵∠ACB=90°,BE平分∠ABC,
∴ED=CE,
∴CE=3cm.
故选C.
C
【解析】∵ED⊥AB,∠A=30°,
∴AE=2ED,
∵AE=6cm,
∴ED=3cm.
∵∠ACB=90°,BE平分∠ABC,
∴ED=CE,
∴CE=3cm.
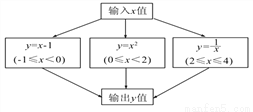
故选C. 根据下图所示程序计算函数值,若输入的x的值为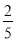 ,则输出的函数值为( )
,则输出的函数值为( )
A. 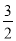 B.
B. 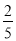 C.
C.  D.
D. 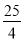
 C
【解析】试题分析:∵x=,
∴0≤x<2,
把x=代入y=x2得
y==,
故选C.
C
【解析】试题分析:∵x=,
∴0≤x<2,
把x=代入y=x2得
y==,
故选C. (c-a2b2)2 等于( )
A. c -ab2 B. c2 -2a2b2c+a4b4 C. c-a2b2c+a4b4 D. c2 -2abc+a4b
 B
【解析】根据完全平方公式可得:(c-a2b2)2=c2 -2a2b2c+a4b4 ,故选B.
B
【解析】根据完全平方公式可得:(c-a2b2)2=c2 -2a2b2c+a4b4 ,故选B. (x+5y)2 等于( )
A. x2-5y 2 B. x2-10y+5y 2 C. x2+10xy+25y 2 D. x2-y+25y 2
 C
【解析】根据完全平方公式可得:(x+5y)2=x2+10xy+25y 2 ,故选C.
C
【解析】根据完全平方公式可得:(x+5y)2=x2+10xy+25y 2 ,故选C. 102×98等于_______;
 9996
【解析】102×98=(100+2)×(100-2)=10000-4=9996.
9996
【解析】102×98=(100+2)×(100-2)=10000-4=9996. [c+(a2)2][c-(a2)2]等于( )
A. c -a2 B. c2 -a8 C. c2 -a2 D. c2 -a4
 B
【解析】根据平方差公式和幂的乘方法则可得:[c+(a2)2][c-(a2)2]= =c2 -a8,故选B.
B
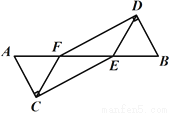
【解析】根据平方差公式和幂的乘方法则可得:[c+(a2)2][c-(a2)2]= =c2 -a8,故选B. 如图, 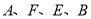 四点共线,
四点共线, 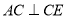 ,
, 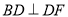 ,
, 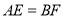 ,
, 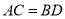 .求证:CE∥DF.
.求证:CE∥DF.
 证明见解析.
【解析】试题分析:利用HL证明RtΔACE?RtΔBDF,根据全等三角形的性质即可得∠AEC=∠BFD,由内错角相等,两直线平行即可得CE∥DF.
试题解析:
∵AC⊥CE,BD⊥DF,
∴∠ACE=∠BDF=90°,
又∵AE=BF,AC=BD,
∴RtΔACE?RtΔBDF(HL),
∴∠AEC=∠BFD,
∴CE∥DF.
...
证明见解析.
【解析】试题分析:利用HL证明RtΔACE?RtΔBDF,根据全等三角形的性质即可得∠AEC=∠BFD,由内错角相等,两直线平行即可得CE∥DF.
试题解析:
∵AC⊥CE,BD⊥DF,
∴∠ACE=∠BDF=90°,
又∵AE=BF,AC=BD,
∴RtΔACE?RtΔBDF(HL),
∴∠AEC=∠BFD,
∴CE∥DF.
... 下列式子中,属于分式的是( )
A. 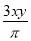 B.
B. 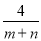 C.
C. 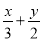 D.
D. 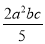
 B
【解析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
【解析】
A、是整式;
B、是分式;
C、是整式;
D、是整式.
故选B.
B
【解析】判断分式的依据是看分母中是否含有字母,如果含有字母则是分式,如果不含有字母则不是分式.
【解析】
A、是整式;
B、是分式;
C、是整式;
D、是整式.
故选B.