题目内容
20. 某人沿坡度为1:3的斜坡从坡底A处行走至坡顶B处,已知AB=3$\sqrt{10}$米,在B处测得AD延长线上一物体C的俯角α为37°,求坡底A到物体C的距离.
某人沿坡度为1:3的斜坡从坡底A处行走至坡顶B处,已知AB=3$\sqrt{10}$米,在B处测得AD延长线上一物体C的俯角α为37°,求坡底A到物体C的距离.(Sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,$\sqrt{10}$≈3.17)
分析 设BD=x,AD=3x根据勾股定理得到BD=3,AD=9,解直角三角形即可得到结论.
解答 解:设BD=x,AD=3x,
∵BD2+AD2=AB2,
即x2+(3x)2=(3$\sqrt{10}$)2,
解得:x=3,
∴BD=3,AD=9,
∵α=37°,
∴∠BCD=37°,
∵tan∠BCD=$\frac{BD}{DC}$,即$\frac{3}{DC}$=0.75,
∴DC=4,
∴AC=AD+DC=9+4=13,
答:坡底A到物体C的距离为13米.
点评 本题考查解直角三角形的应用-仰角俯角问题及坡度坡角问题,难度适中.要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
10.下列四组数,可作为直角三角形三边长的是( )
| A. | 5cm、12cm、13cm | B. | 1cm、2cm、3cm | C. | 2cm、3cm、4cm | D. | 4cm、5cm、6cm |
5. 如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )
如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )
 如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )
如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
12.方程3x+2y=17在自然数范围内的解( )
| A. | 有无数组 | B. | 只有1组 | C. | 只有3组 | D. | 只有4组 |
10.把方程3x+y=2,写成用含y的形式为( )
| A. | x=$\frac{y-2}{3}$ | B. | x=$\frac{2-y}{3}$ | C. | y=3x-2 | D. | y=2-3x |
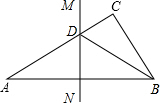 如图,直线MN是△ABC的边AB的垂直平分线,MN交AC于点D,连接BD,若AC=6cm,BC=4,AB=7cm,则△BCD的周长为10cm.
如图,直线MN是△ABC的边AB的垂直平分线,MN交AC于点D,连接BD,若AC=6cm,BC=4,AB=7cm,则△BCD的周长为10cm.