题目内容
15．解下列方程：$\frac{x}{x-2}=2+\frac{3}{x-3}$．分析 两边都乘以（x-2）（x-3），去分母化分式方程为整式方程，解整式方程可得x的值，最后检验可得．
解答 解：两边都乘以（x-2）（x-3），得：x=2（x-2）（x-3）+3，
整理，得：2x2-11x+15=0，
因式分解，得：（x-3）（2x-5）=0，
解得：x=3或x=2.5，
检验：当x=3时，（x-2）（x-3）=0，
当x=2.5时，（x-2）（x-3）=-$\frac{1}{4}$≠0，
∴原分式方程的解为x=2.5．
点评 本题考查了解分式方程．注意：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．（2）解分式方程一定注意要验根．
练习册系列答案
相关题目
5．
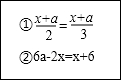数学老师在如图所示的木板上写了关于x的两个方程，并解出方程①的解比方程②的解小4，则a的值为（ ）
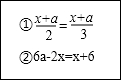数学老师在如图所示的木板上写了关于x的两个方程，并解出方程①的解比方程②的解小4，则a的值为（ ）| A． | $\frac{3}{2}$ | B． | $-\frac{3}{2}$ | C． | 2 | D． | -2 |
10．下列四组数，可作为直角三角形三边长的是（ ）
| A． | 5cm、12cm、13cm | B． | 1cm、2cm、3cm | C． | 2cm、3cm、4cm | D． | 4cm、5cm、6cm |
20．
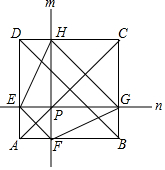如图，P为边长为4的正方形ABCD的对角线AC上动点（不与A、C重合），过P作直线m、n，分别与AD、AB平行，与正方形各边分别交于E、F、G、H，在以下判断中，不正确的是（ ）
如图，P为边长为4的正方形ABCD的对角线AC上动点（不与A、C重合），过P作直线m、n，分别与AD、AB平行，与正方形各边分别交于E、F、G、H，在以下判断中，不正确的是（ ）| A． | P点变化时，四边形EFGH面积保持不变 | |
| B． | P点变化时，六边形DEFBGH面积有最大值12$\sqrt{2}$ | |
| C． | 点P位于正方形ABCD的中心时，DE=2 | |
| D． | P点变化时，六边形DEFBGH周长保持不变 |
7．
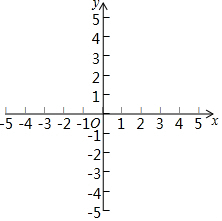数学李老师给学生出了这样一个问题：探究函数y=$\frac{x}{x+1}$图象与性质．小斌根据学习函数的经验，对函数y=$\frac{x}{x+1}$的图象与性质进行了探究．下面是小斌的探究过程，请补充完成：
（1）函数y=$\frac{x}{x+1}$的自变量x的取值范围是x≠-1；
（2）根据下表所列出y与x对应值，在平面直角坐标系中描出各对以对应值为坐标的点，并画出该函数的图象；
（3）若直线y=x+b与函数y=$\frac{x}{x+1}$的图象无交点，请直接写出b的取值范围．
数学李老师给学生出了这样一个问题：探究函数y=$\frac{x}{x+1}$图象与性质．小斌根据学习函数的经验，对函数y=$\frac{x}{x+1}$的图象与性质进行了探究．下面是小斌的探究过程，请补充完成：（1）函数y=$\frac{x}{x+1}$的自变量x的取值范围是x≠-1；
（2）根据下表所列出y与x对应值，在平面直角坐标系中描出各对以对应值为坐标的点，并画出该函数的图象；
（3）若直线y=x+b与函数y=$\frac{x}{x+1}$的图象无交点，请直接写出b的取值范围．
| x | … | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | 3 | 4 | 5 | … |
| y | … | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | … |
5．
如图，已知直线l1∥l2，将等边三角形如图放置，若∠α=40°，则∠β等于（ ）
如图，已知直线l1∥l2，将等边三角形如图放置，若∠α=40°，则∠β等于（ ）| A． | 20° | B． | 30° | C． | 40° | D． | 50° |