题目内容
1.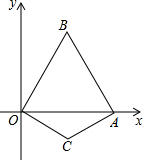 已知:如图,在直角坐标系xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请写出所有符合条件的点D的坐标($\frac{\sqrt{3}}{3}$,1),($\frac{2\sqrt{3}}{3}$0),($\frac{2}{3}$,0),($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).
已知:如图,在直角坐标系xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请写出所有符合条件的点D的坐标($\frac{\sqrt{3}}{3}$,1),($\frac{2\sqrt{3}}{3}$0),($\frac{2}{3}$,0),($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).
分析 如果△OCD为等腰三角形,那么分点D在OA边或者OB边上或AB边上三种情形.每一种情形,都有可能O为顶点,C为顶点,D为顶点,分别讨论,得出结果.
解答  解;如图1,若点D在OA上时,OC=OD,则OD=OC=$\frac{2\sqrt{3}}{3}$,
解;如图1,若点D在OA上时,OC=OD,则OD=OC=$\frac{2\sqrt{3}}{3}$,
D点的坐标为($\frac{2\sqrt{3}}{3}$,0),
如图2,若OD=CD时,
∵∠COD=30°,cos∠COD=$\frac{DQ}{OD}$,
∴cos30°=$\frac{DQ}{OD}$,
∴OD=$\frac{OQ}{cos30°}$=$\frac{2}{3}$,
∴D点的坐标为($\frac{2}{3}$,0);
如图2,当点D在BA上时,
若OD=CD,则点D在OC的垂直平分线上,设OC的垂直平分线DQ与x轴交于点P,
则∠APD=60°,OQ=CQ=$\frac{\sqrt{3}}{3}$,
∵∠DAP=60°,
∴△ADP是等边三角形,
过点D作DM⊥PA于M,则PM=DM,
∵∠AOC=30°,
∴OP=$\frac{OQ}{cos30°}$=$\frac{2}{3}$,
∴AP=2-$\frac{2}{3}$=$\frac{4}{3}$,
∴PM=$\frac{2}{3}$,
∴OM=$\frac{4}{3}$,DM=tan60°•PM=$\frac{2\sqrt{3}}{3}$,
∴D点的坐标为($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$);
如图4,当点D在OB上时,
若OD=OC,则OD=$\frac{2\sqrt{3}}{3}$,
过点D作DM⊥OA于M,则OM=$\frac{1}{2}$OD=$\frac{\sqrt{3}}{3}$,DM=1,
则D点的坐标为($\frac{\sqrt{3}}{3}$,1);
综上所述;符合条件的点D的坐标是($\frac{\sqrt{3}}{3}$,1)或($\frac{2\sqrt{3}}{3}$0)或($\frac{2}{3}$,0)或($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).
点评 本题主要考查了等腰三角形、等边三角形的性质,全等三角形的判定,关键是根据题意画出图形,注意分类讨论时,做到不重复,不遗漏.

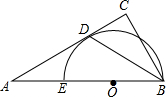 如图,在△ABC中,∠C=90°,BD平分∠ABC,E是AB上的一点,以BE为直径的⊙O过点D.
如图,在△ABC中,∠C=90°,BD平分∠ABC,E是AB上的一点,以BE为直径的⊙O过点D.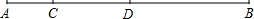 如图,点C、D在线段AB上,D是线段AB的中点,AC=$\frac{1}{3}$AD,AB=12,求线段CD的长.
如图,点C、D在线段AB上,D是线段AB的中点,AC=$\frac{1}{3}$AD,AB=12,求线段CD的长. 如图,射线OA表示北偏东35°,射线OB表示南偏东70°.
如图,射线OA表示北偏东35°,射线OB表示南偏东70°.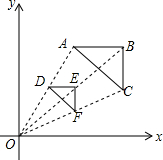 如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )
如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )