题目内容
6.观察下列各式:$\frac{1}{1×4}=(1-\frac{1}{4})×\frac{1}{3}$
$\frac{1}{4×7}$=($\frac{1}{4}$-$\frac{1}{7}$)×$\frac{1}{3}$
$\frac{1}{7×10}$=($\frac{1}{7}$-$\frac{1}{10}$)×$\frac{1}{3}$
利用你所发现的规律尝试计算下式:$\frac{1}{1×4}+\frac{1}{4×7}+\frac{1}{7×10}+…+\frac{1}{100×103}$.
分析 分子是1,分母是相差3的两个自然数的乘积,可以拆成以这两个自然数为分母,分子是1的两个分数差的$\frac{1}{3}$,由此规律拆分计算即可.
解答 解:$\frac{1}{1×4}+\frac{1}{4×7}+\frac{1}{7×10}+…+\frac{1}{100×103}$
=$\frac{1}{3}$×(1-$\frac{1}{4}$)+$\frac{1}{3}$×($\frac{1}{4}$-$\frac{1}{7}$)+$\frac{1}{3}$×($\frac{1}{7}$-$\frac{1}{10}$)+…+$\frac{1}{3}$×($\frac{1}{100}$-$\frac{1}{103}$)
=$\frac{1}{3}$×(1-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{7}$+$\frac{1}{7}$-$\frac{1}{10}$+…+$\frac{1}{100}$-$\frac{1}{103}$)
=$\frac{1}{3}$×(1-$\frac{1}{103}$)
=$\frac{1}{3}$×$\frac{102}{103}$
=$\frac{34}{103}$.
点评 此题考查数字的变化规律,注意分子与分母之间的联系,找出计算的规律拆分,掌握拆分前后分数的大小不能变.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.当x=-2时,分式$\frac{{x}^{2}-4}{3x-1}$的值是( )
| A. | 0 | B. | 无意义 | C. | 1 | D. | $\frac{1}{7}$ |
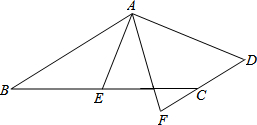 已知,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.
已知,AB∥DC,E为BC边的中点,∠BAE=∠EAF,AF与DC的延长线相交于点F.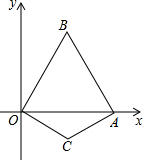 已知:如图,在直角坐标系xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请写出所有符合条件的点D的坐标($\frac{\sqrt{3}}{3}$,1),($\frac{2\sqrt{3}}{3}$0),($\frac{2}{3}$,0),($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).
已知:如图,在直角坐标系xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请写出所有符合条件的点D的坐标($\frac{\sqrt{3}}{3}$,1),($\frac{2\sqrt{3}}{3}$0),($\frac{2}{3}$,0),($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).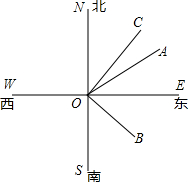 如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余
如图,直线SN与直线WE相交于点O,射线ON表示正北方向,射线OE表示正东方向.已知射线OB的方向是南偏东m°,射线OC的方向是北偏东n°,且m°的角与n°的角互余