题目内容
11.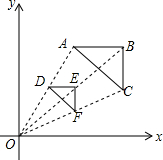 如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )
如图,△ABC中,A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,若D(1,2),△DEF的面积为4,则△ABC的面积为( )| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
分析 利用位似图形的性质结合对应点坐标得出位似比,进而求出△ABC的面积.
解答 解:∵A(2,4)以原点为位似中心,将△ABC缩小后得到△DEF,D(1,2),
∴位似比为:2:1,
∵△DEF的面积为4,
∴△ABC的面积为:4×4=16.
故选:D.
点评 此题主要考查了位似变换以及坐标与图形的性质,得出两图形的位似比是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.当x=-2时,分式$\frac{{x}^{2}-4}{3x-1}$的值是( )
| A. | 0 | B. | 无意义 | C. | 1 | D. | $\frac{1}{7}$ |
3.下列计算正确的是( )
| A. | a3+a2=a5 | B. | a3•a2=a6 | C. | (a3)2=a9 | D. | a6÷a2=a4 |
20.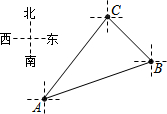 如图,一张地图上有A、B、C三地,C地在A地的北偏东38°方向,在B地的西北方向,则∠ACB等于( )
如图,一张地图上有A、B、C三地,C地在A地的北偏东38°方向,在B地的西北方向,则∠ACB等于( )
 如图,一张地图上有A、B、C三地,C地在A地的北偏东38°方向,在B地的西北方向,则∠ACB等于( )
如图,一张地图上有A、B、C三地,C地在A地的北偏东38°方向,在B地的西北方向,则∠ACB等于( )| A. | 73° | B. | 83° | C. | 90° | D. | 97° |
1.要使$\frac{{\sqrt{2x-4}}}{x-3}$有意义,则x的取值范围是( )
| A. | x<2 | B. | x≥2 | C. | x≥2且x≠3 | D. | x>2且x≠3 |
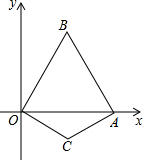 已知:如图,在直角坐标系xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请写出所有符合条件的点D的坐标($\frac{\sqrt{3}}{3}$,1),($\frac{2\sqrt{3}}{3}$0),($\frac{2}{3}$,0),($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).
已知:如图,在直角坐标系xOy中,边长为2的等边△OAB的顶点B在第一象限,顶点A在x轴的正半轴上.另一等腰△OCA的顶点C在第四象限,OC=AC,∠C=120°.在等边△OAB的边上(点A除外)存在点D,使得△OCD为等腰三角形,请写出所有符合条件的点D的坐标($\frac{\sqrt{3}}{3}$,1),($\frac{2\sqrt{3}}{3}$0),($\frac{2}{3}$,0),($\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$).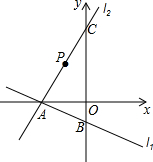 已知直线l1的解析式为y=-$\frac{1}{3}$x-2,且与x轴,y轴分别交于A、B两点,点C在y轴上,且点C的纵坐标为x2-7x-8=0中较大的解,直线l2过A、C两点.
已知直线l1的解析式为y=-$\frac{1}{3}$x-2,且与x轴,y轴分别交于A、B两点,点C在y轴上,且点C的纵坐标为x2-7x-8=0中较大的解,直线l2过A、C两点. 如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB为72°.
如图,在△ABC中,AB=AC,∠A=36°,∠1=∠2,∠ADE=$\frac{1}{2}$∠EDB,则∠DEB为72°.