题目内容
20．
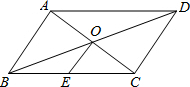如图，平行四边形ABCD中，对角线AC、BD交于点O，点E是BC的中点．若OE=3cm，则AB的长为（ ）| A． | 3cm | B． | 6cm | C． | 9cm | D． | 12cm |
分析 因为四边形ABCD是平行四边形，所以OA=OC；又因为点E是BC的中点，所以OE是△ABC的中位线，由OE=3cm，即可求得AB=6cm．
解答 解：∵四边形ABCD是平行四边形，
∴OA=OC；
又∵点E是BC的中点，
∴BE=CE，
∴AB=2OE=2×3=6（cm）
故选：B．
点评 此题考查了平行四边形的性质：平行四边形的对角线互相平分．还考查了三角形中位线的性质：三角形的中位线平行且等于三角形第三边的一半．
练习册系列答案
相关题目
11．如果$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax+by=0}\\{bx-cy=1}\end{array}\right.$的解，那么，下列各式中成立的是（ ）
| A． | a+4c=2 | B． | 4a+c=2 | C． | a+4c+2=0 | D． | 4a+c+2=0 |
15．
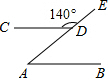如图，AB∥CD，∠CDE=140°，则∠A的度数为（ ）
如图，AB∥CD，∠CDE=140°，则∠A的度数为（ ）| A． | 70° | B． | 65° | C． | 50° | D． | 40° |
5．在下列实数中，无理数是（ ）
| A． | 0.151515… | B． | π | C． | -4 | D． | $\frac{22}{9}$ |
（1）如图，已知∠1=∠2，求证：a∥b．