题目内容
1．
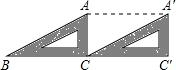如图，将三角尺ABC沿BC方向平移，得到三角形A′CC′．已知∠B=30°，∠ACB=90°，则∠BAA′的度数为150°．
分析 根据平移的性质，可得AA′与BC的关系，根据平行线的性质，可得答案．
解答 解：由将三角尺ABC沿BC方向平移，得到三角形A′CC′，得
AA′∥BC．
由AA′∥BC，
得∠BAA′+∠B=180°．
由∠B=30°，得
∠BAA′=150°．
故答案为：150°．
点评 本题考查了平移的性质，利用了平移的性质：对应点所连的线段平行或在同一条直线上．
练习册系列答案
相关题目
11．如果$\left\{\begin{array}{l}{x=-1}\\{y=2}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax+by=0}\\{bx-cy=1}\end{array}\right.$的解，那么，下列各式中成立的是（ ）
| A． | a+4c=2 | B． | 4a+c=2 | C． | a+4c+2=0 | D． | 4a+c+2=0 |
12．定义：直线l1与l2相交于点O，对于平面内任意一点P1点P到直线l1与l2的距离分别为p、q则称有序实数对（p，q）是点P的“距离坐标”．根据上述定义，“距离坐标”是（3，2）的点的个数有4个．
（1）如图，已知∠1=∠2，求证：a∥b．
16．小米同学乘坐一艘游船出海游玩，游船上的雷达扫描探测得到的结果如图所示，每相邻两个圆之间距离是1km（小圆半径是1km），若小艇C相对于游船的位置可表示为（0°，-1.5），请你描述图中另外两个小艇A、B的位置，正确的是（ ）
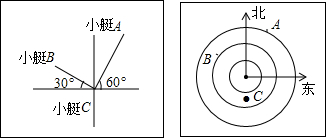
| A． | 小艇A（60°，3），小艇B（-30°，2） | B． | 小艇A（30°，4），小艇B（-60°，3） | ||
| C． | 小艇A（60°，3），小艇B（-30°，3） | D． | 小艇A（30°，3），小艇B（-60°，2） |
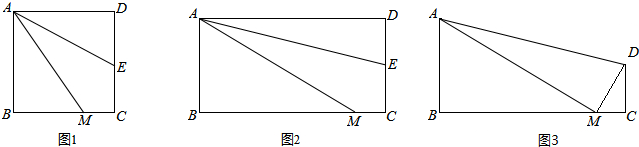
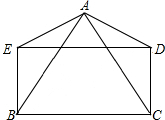如图，?BCDE中，EA⊥AC于A，BA⊥AD于A，求证：四边形BCDE是矩形．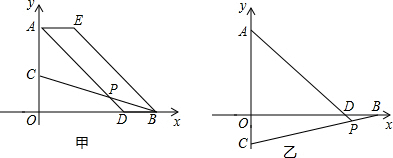
如图所示，矩形纸片ABCD中，AB=5cm，点E在BC上，且AE=EC．若将纸片沿AE折叠，点B恰好与AC上的点B′重合，则AC=10 cm．